개요
딥 러닝은 인공 신경망을 구성하여 주어진 문제를 해결한다. 인공 신경망은 사람의 뇌를 모사하기 위한 시도에서 출발했는데, 오늘은 이 중 인간의 뉴런을 모사한 존재인 퍼셉트론 (Perceptron)에서부터 딥 러닝에 대한 설명을 시작하려고 한다.
뉴런
뉴런 자체에 대해서는 앞선 포스트에서도 잠깐 설명했지만, 인간의 신경 세포로서 다른 뉴런을 통해서 입력 신호를 받아 이 신호를 또 다른 뉴런으로 전달하는 역할을 한다. 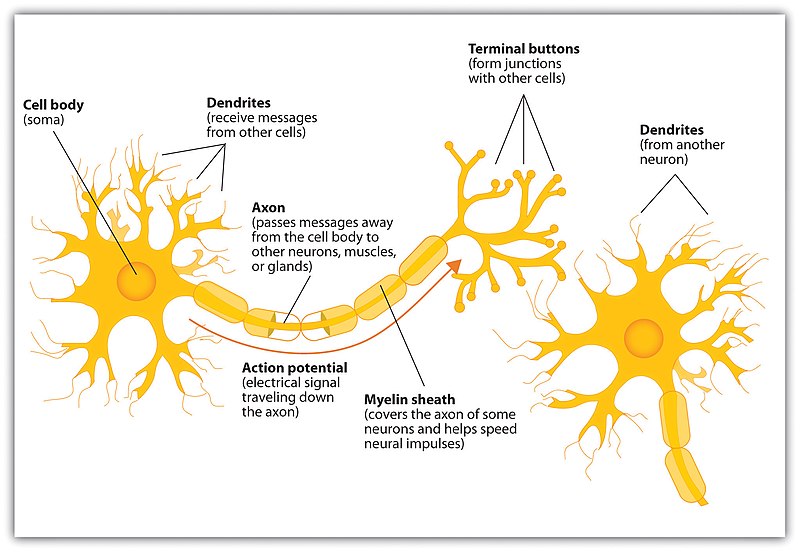 From https://en.wikipedia.org/wiki/Neuron
From https://en.wikipedia.org/wiki/Neuron
퍼셉트론 - 인공 뉴런
퍼셉트론은 뉴런을 수학적으로 표현한 인공 뉴런으로 볼 수 있다. 주어진 입력을 받아서 각각의 가중치를 곱한 뒤, 그의 합을 구한다. 이후 계산한 합을 Threshold(기준치)와 비교해서, 기준치보다 작은 경우 0을 출력하고 기준치보다 큰 경우에는 1을 출력한다.
\[Y = \begin{cases} 1 & if\; \sum_i w_ix_i > T \\0 & if\; \sum_i w_ix_i \leq T \end{cases}\]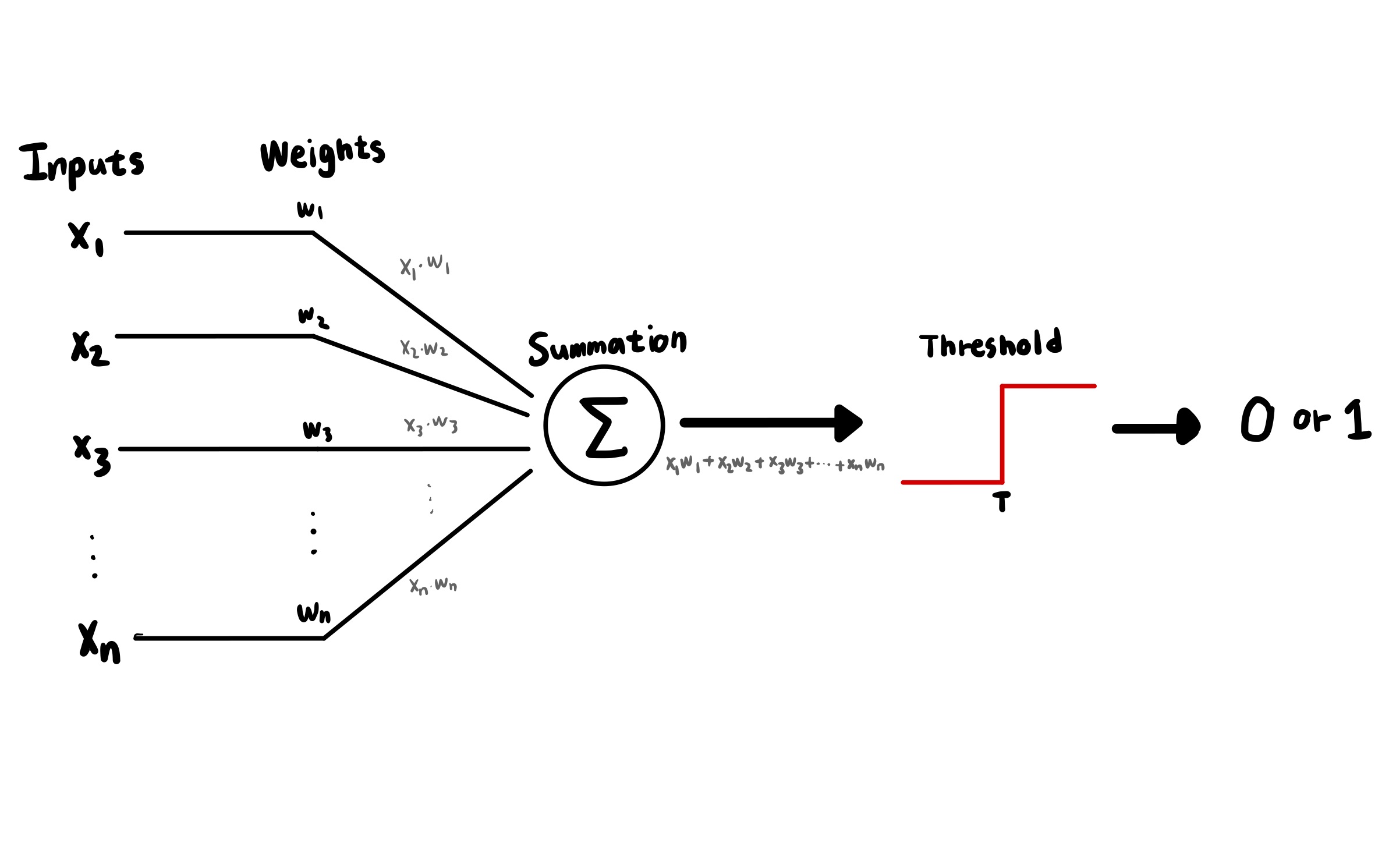
파이썬 코드로 퍼셉트론을 구현하기
앞서 소개한 퍼셉트론의 개념을 파이썬을 통해서 구현할 수 있다!
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
import numpy as np
class Perceptron:
def __init__(self, w, threshold=0.5):
self.weight = w
self.threshold = threshold
def work(self, x):
sum = np.sum(self.weight * x)
if sum <= self.threshold:
return 0
else: # sum > self.threshold
return 1
AND_weight = np.array([0.5, 0.5])
AND_threshold = 0.7
OR_weight = np.array([0.5, 0.5])
OR_threshold = 0.3
NAND_weight = np.array([-0.5, -0.5])
NAND_threshold = -0.7
AND = Perceptron(AND_weight, AND_threshold)
OR = Perceptron(OR_weight, OR_threshold)
NAND = Perceptron(NAND_weight, NAND_threshold)
for input in [(0, 0), (0, 1), (1, 0), (1, 1)]:
AND_output = AND.work(np.array([input[0], input[1]]))
OR_output = OR.work(np.array([input[0], input[1]]))
NAND_output = NAND.work(np.array([input[0], input[1]]))
print(str(input) + ": " + "AND = " + str(AND_output) + ", OR = " + str(NAND_output) + ", NAND = " + str(NAND_output))
실행 결과
(0, 0): AND = 0, OR = 0, NAND = 1
(0, 1): AND = 0, OR = 1, NAND = 1
(1, 0): AND = 0, OR = 1, NAND = 1
(1, 1): AND = 1, OR = 1, NAND = 0
퍼셉트론을 이용해서 논리 게이트 중 AND 게이트와 OR 게이트, NAND 게이트를 구현해 보았다.
AND 게이트는 두 입력이 모두 1일때 1이 출력되고, 나머지 경우에는 0이 출력된다.
OR 게이트는 둘 중 하나만 1이 있다면 1이 출력되고, 둘 모두 0일 때에만 0이 출력된다.
NAND 게이트는 NOT AND의 줄임말로, AND 게이트가 두 입력이 모두 1일때는 0을, 나머지 경우에는 1을 출력한다.
| AND | OR | NAND | |
|---|---|---|---|
| (0, 0) | 0 | 0 | 1 |
| (0, 1) | 0 | 1 | 0 |
| (1, 0) | 0 | 1 | 0 |
| (1, 1) | 1 | 1 | 0 |
그림으로 보자면, 우리는 퍼셉트론을 통해서 주어진 입력을 분류하는 직선을 그은 것과 마찬가지다. 이런 직선을 결정 경계 (Decision boundary)라고 한다.
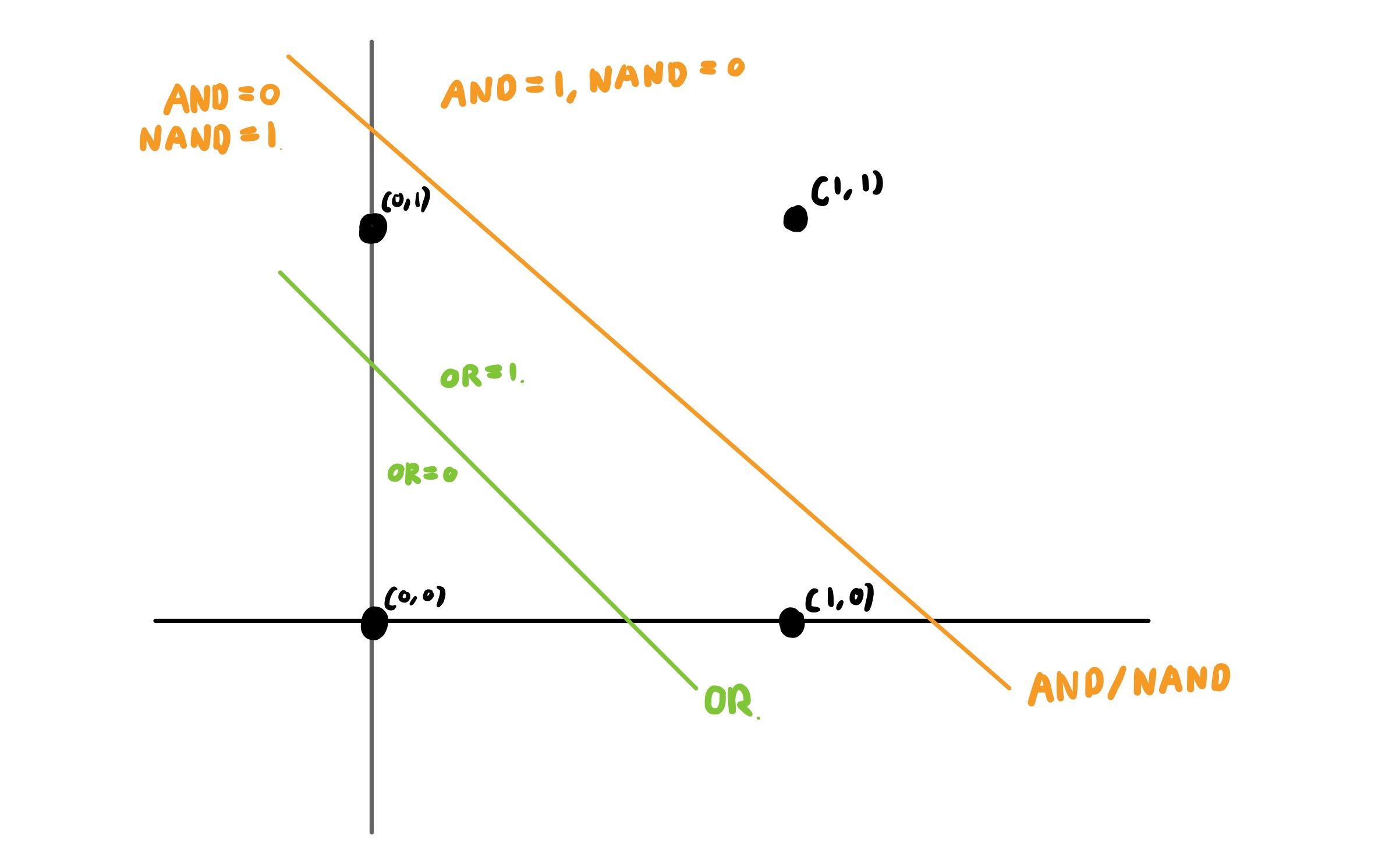
퍼셉트론 식을 변형시키기 - Bias
Bias는 편향이라고도 하는데, 원래 퍼셉트론의 수식을 변형시켜서 얻을 수 있다.
\[Y = \begin{cases} 1 & if\; \sum_i w_ix_i > T \\0 & if\; \sum_i w_ix_i \leq T \end{cases}\] \[Y = \begin{cases} 1 & if\; \sum_i w_ix_i-T > 0 \\0 & if\; \sum_i w_ix_i -T \leq 0 \end{cases}\] \[Y = \begin{cases} 1 & if\; z > 0 \\0 & if\; z \leq 0 \end{cases} \\ where\; z = \sum_i w_ix_i - T\]이때, -T를 Bias로 보며 b라고도 표현한다.
\[z = \sum_i w_ix_i + b \\ where \; b = -T\]한번 더 식을 변형시켜, Bias b를 입력으로 1이 곱해지는 가중치로 볼 수도 있다.
\[z = \sum_i w_ix_i \\ where \; b = 1 \times w_{n+1}\]Bias가 직접적으로 명시되어 있지 않더라도, 입력이 1로 고정되어 있는 가중치가 Bias로서 추가적으로 존재한다고 볼 수 있다.
퍼셉트론의 한계
| XOR | |
|---|---|
| (0, 0) | 0 |
| (0, 1) | 1 |
| (1, 0) | 1 |
| (1, 1) | 0 |
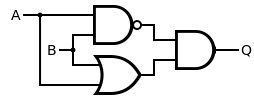
XOR 게이트는 두 입력이 서로 다를때 1을, 서로 같은 경우에는 0을 출력하는 논리 게이트이다. 이런 게이트를 퍼셉트론을 이용해서 구현할 수 있을까? 다르게 표현하면 하나의 직선으로 (0,0)&(1,1)과 (0,1)&(1,0)을 분리할 수 있을까? 아쉽지만 그런 방법은 없다. 퍼셉트론 하나로 구현할 수 없는 논리 게이트도 있는 것이다. 게다가 우리 실생활의 데이터를 분류할 때, 칼로 무 자르듯 일직선으로 분류할 수 없는 데이터가 훨씬 더 많기에 단순한 퍼셉트론으로는 문제를 해결할 수 없다는 점이 드러나자 AI 기술은 한동안 침체를 피할 수 없었다. 이 기간을 AI의 첫번째 겨울이라고 한다.
해결책
그렇다면 아무런 방법이 없었을까? 만약 이 지점에서 기술의 발전이 멈추었다면 지금의 인공지능은 없었을 것이다. 이 포스트에서는 하나의 그림만 보여드리고자 한다.