개요

지난 포스트에서 우리는 퍼셉트론과 그 한계점에 대해서 알아봤다. 그 한계점이란 퍼셉트론 하나로는 데이터를 적절하게 분류할 수 없는 경우도 있다는 것이다. 이번에는 이러한 문제를 해결하기 위해 제안된 Multi Layer Perceptron에 대해서 알아본다.

Multi Layer Perceptron

Multi Layer Perceptron이라는 말을 해석하면 다층 퍼셉트론이라는 뜻이다. 즉 여러 개의 퍼셉트론을 엮어서 구성한 신경망이라고 할 수 있는데, 인간의 뇌가 뉴런 하나로 구성된 것이 아니라 여러 개의 뉴런이 연결되어 있다는 점을 생각하면 조금 더 사람의 뇌에 가까운 형상이라고 할 수 있겠다.

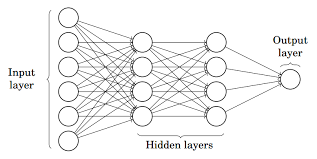
From https://medium.com/@temi.ayo.babs/multi-layer-perceptron-for-beginners-6aee246c6a03

입력 역시 하나의 Layer로 보고 Input layer로 정의한다. 위 그림에서는 입력 데이터가 총 6개 있다고 볼 수 있다. 이후 각각 4개의 퍼셉트론으로 구성된 Hidden Layer가 2개, 마지막으로 Output Layer가 있다.

한편, 중요한 것은 같은 Layer 내의 퍼셉트론끼리는 그림에서도 보다시피 연결이 전혀 없고, 이에 따라 데이터를 주고받지 않는다는 점이다.

파이썬을 이용해 XOR 게이트 구현하기

지난 포스트에서 보았던 그림을 바탕으로, XOR 게이트를 파이썬을 통해 구현해보고자 한다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

import numpy as np

class Perceptron:
    def __init__(self, w, threshold=0.5):
        self.weight = w
        self.threshold = threshold

    def work(self, x):
        sum = np.sum(self.weight * x)

        if sum <= self.threshold:
            return 0
        else: # sum > self.threshold
            return 1

def MLP_XOR(x):
    AND_weight = np.array([0.5, 0.5])
    AND_threshold = 0.7
    OR_weight = np.array([0.5, 0.5])
    OR_threshold = 0.3
    NAND_weight = np.array([-0.5, -0.5])
    NAND_threshold = -0.7

    AND = Perceptron(AND_weight, AND_threshold)
    OR = Perceptron(OR_weight, OR_threshold)
    NAND = Perceptron(NAND_weight, NAND_threshold)

    # x = input layer
    # h1, h2 = hidden layer
    # y = output layer
    h1 = NAND.work(x)
    h2 = OR.work(x)
    y = AND.work(np.array([h1, h2]))

    return y

for input in [(0, 0), (0, 1), (1, 0), (1, 1)]:
    XOR_output = MLP_XOR(np.array([input[0], input[1]]))

    print(str(input) + ": " + "XOR = " + str(XOR_output))

실행 결과
(0, 0): XOR = 0
(0, 1): XOR = 1
(1, 0): XOR = 1
(1, 1): XOR = 0

지난번 포스트에서 봤던 정의와 마찬가지로 두 입력이 서로 다를때는 1, 서로 같을때는 0이 출력되고 있다.

MLP의 의미

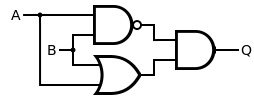
주어진 코드에서 알 수 있듯이, 우리는 XOR 게이트를 구현하기 위해서 NAND 게이트와 OR 게이트의 결과값을 AND 게이트로 합쳤다.

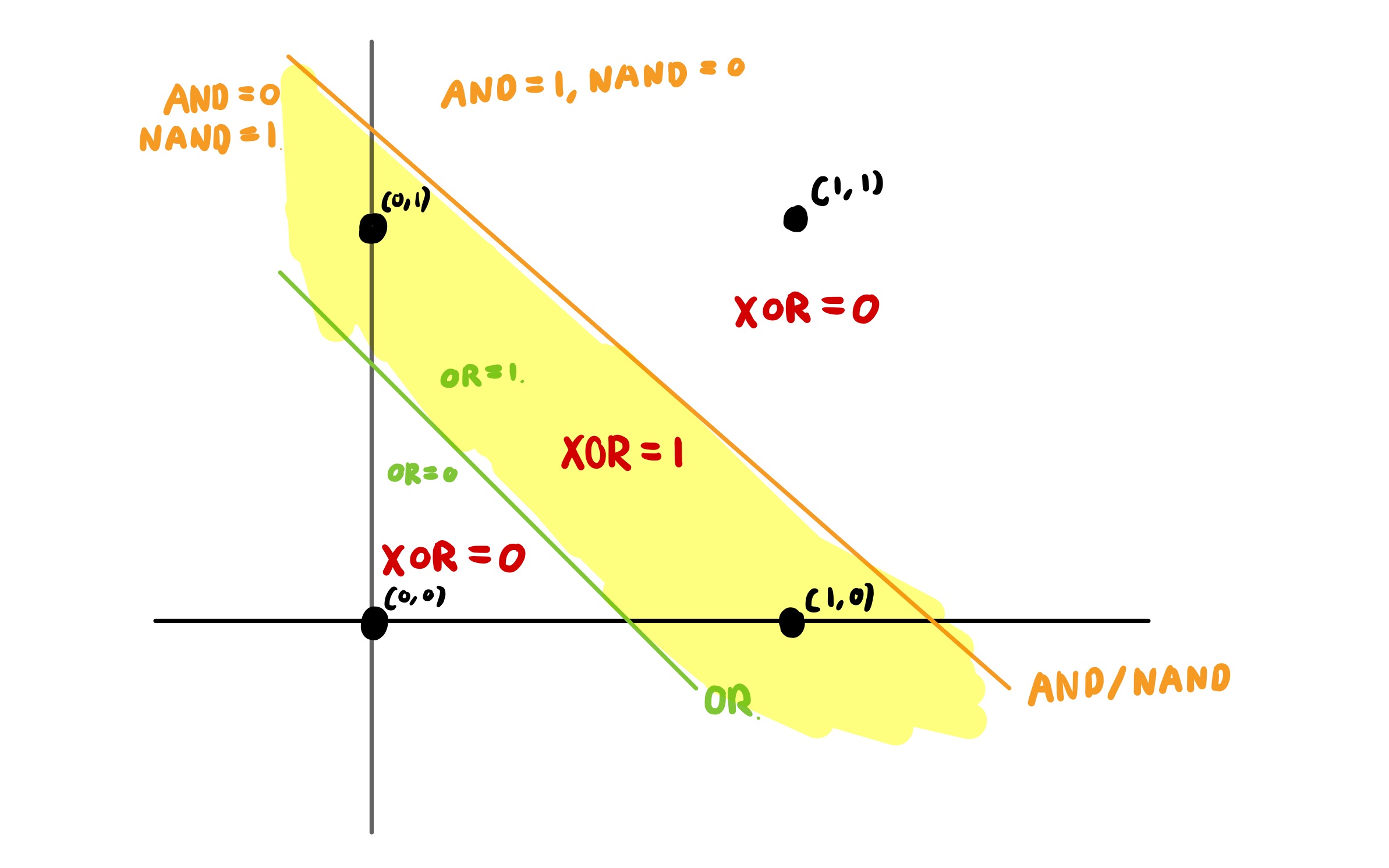
위 그림과 같이, OR 게이트가 1인 구간과 NAND 게이트가 1인 구간을 합쳐, 그 둘 모두가 1인 구간을 표현할 수 있게 된 것이다. 우리는 이제 단순한 직선 이상의 결정 경계 (Decision boundary)를 구현할 수 있게 되었다! 이를 통해서 이미지 등의 주어진 데이터를 분류하는 등의 작업을 무리 없이 수행할 수 있다.

결론

단순히 하나의 퍼셉트론이 아니라 여러 개의 퍼셉트론을 다층적으로 구성한 MLP를 통해 더욱 더 많은 문제를 해결할 수 있다.