개요
지금까지는 퍼셉트론에 단순히 Threshold를 적용했는데, 여기서 더 나아가서 Threshold를 대체하는 Activation function에 대해 알아보고자 한다.
Threshold의 단점
Threshold 함수의 단점을 알아보기 위해서, Threshold 함수를 python의 Matplotlib.pyplot을 이용해 그려 보았다.
1
2
3
4
5
6
7
8
9
10
11
12
13
import numpy as np
import matplotlib.pyplot as plt
def threshold_function(x, threshold=0):
return np.array(x>threshold, dtype=np.int32)
x = np.arange(-10, 10, 0.01)
y = threshold_function(x)
plt.plot(x, y)
plt.grid(True)
plt.show()
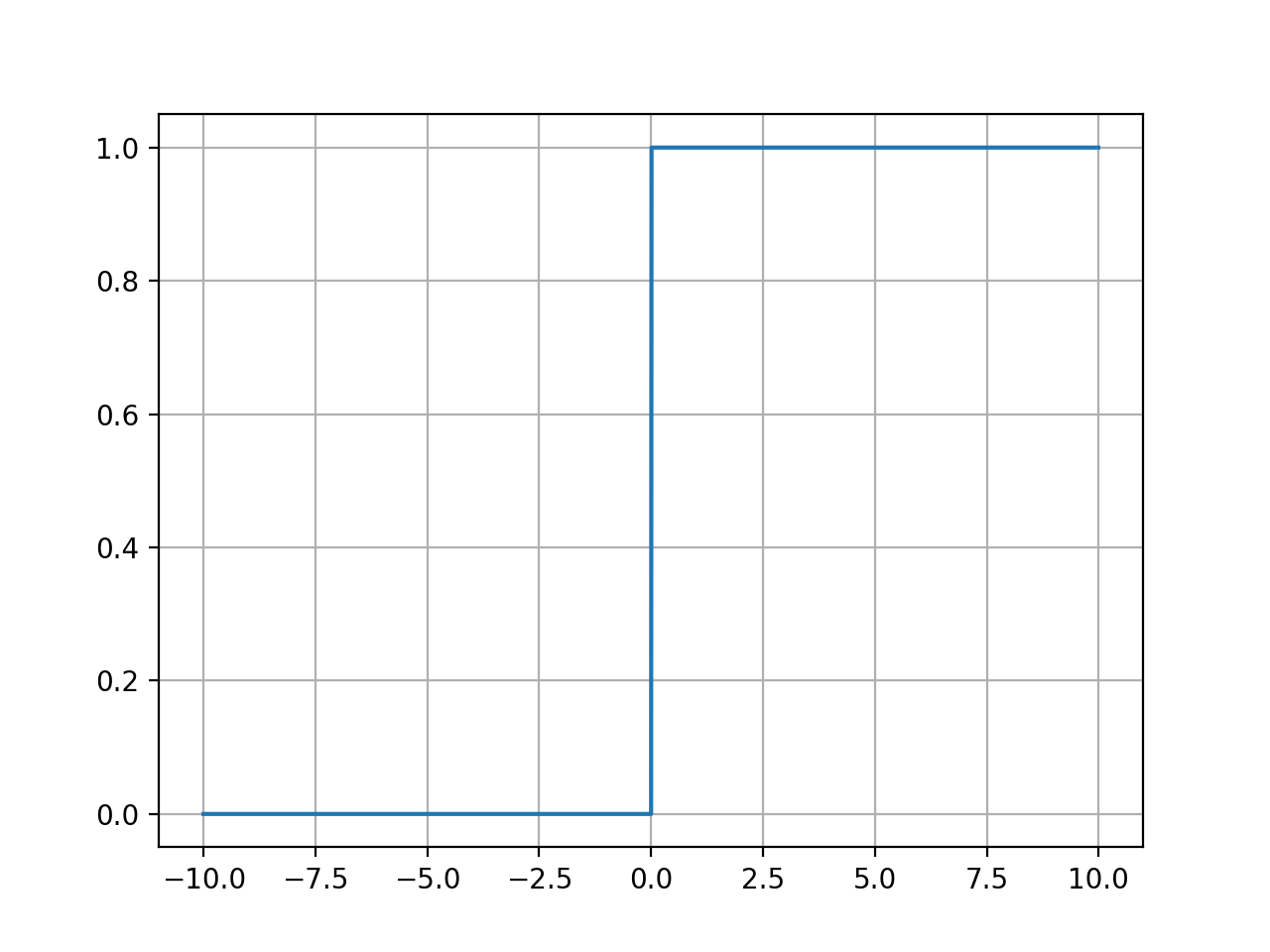
이는 Threshold가 0일때를 기준으로 했는데, 시각적으로 확인할 수 있는 사실은 Threshold를 기준으로 왼쪽은 0, 오른쪽은 1이라는 사실이다.
그런데 세상에 이렇게 칼로 무 자르듯 주어진 데이터를 0과 1로 분류할 수 있는 경우가 얼마나 될까? 결코 많지 않다. 예를 들어서 키를 통해서 성별을 유추해본다고 하면 (모두 성인임을 가정할 때) 키가 160cm 이하이면 무조건 여성일까? 180cm 이상이면 무조건 남성일까? 절대 그렇지 않다. 키에 따라서 사람의 성별을 분류하고자 했을 때 결국 우리가 얻게 되는 것은 키에 따라 특정 성별일 확률이어야 하는 것이다. 키가 큰 사람일수록 분명히 남성일 확률은 높아지지만, 그것이 100%는 아니기 때문이다.
아래 그림의 윗부분이 키에 따른 성별의 분포라고 했을 때, Threshold 함수를 사용하면 그림의 아랫부분처럼 흑백으로 분류할 수 밖에 없다.

이처럼 Threshold 함수를 통해서는 세상을 제대로 표현할 수 없다. 데이터를 단순히 0과 1 두가지로 분류하는 과정에서 정보의 상실이 일어나기 때문이다.
다른 Activation function의 도입
이렇게 정보를 ‘상실’하는 문제를 보완하기 위해서, Threshold 대신 다른 함수를 이용하는 방법이 고안되었다. Threshold 함수를 포함해 이 함수들을 Activation function이라고 하는데, 여기에는 어떤 것이 있는지 알아보겠다.
Sigmoid 함수
Sigmoid 함수는 Logistic 함수라고도 하는데, 그 식은 아래와 같다.
\[\sigma(z) = \frac{1}{1 + exp(-z)} \\ where \; z = \sum_i w_ix_i + b\]입력과 가중치의 곱에 편향을 반영한 (이 과정을 Affine comvbination 또는 Affine transformation이라고 한다) z를 식에 집어넣는다.
이 식에 따라 Threshold 함수와 마찬가지로 그래프를 그려 보면 아래와 같은 결과가 나온다.
1
2
def sigmoid(x):
return 1 / (1 + np.exp(-x))
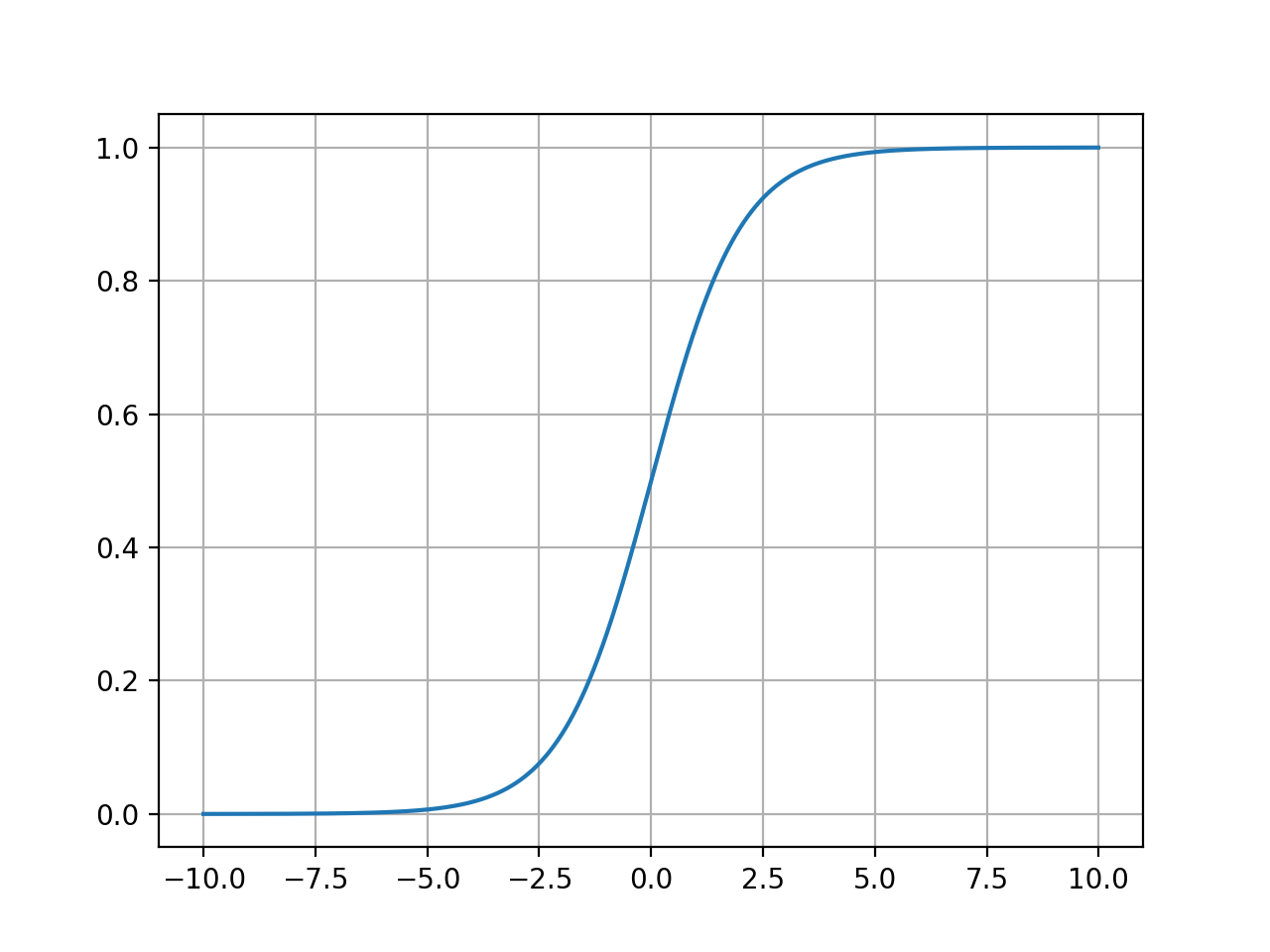
이 그래프를 관찰하면 다음 사실을 알 수 있다.
- 출력이 0과 1 사이로 제한된다.
- 입력이 작을 수록 출력이 0에 가깝고, 클 수록 1에 가깝다.
이 Sigmoid 함수의 출력값은 입력에 따른 출력의 확률이라고 볼 수 있다. 다시 키에 따른 성별 분류 예시로 돌아가 보자면, 이 그래프는 키가 클수록 성별이 남성일 확률이 높아지는 현상을 나태나고 있는 것이다.
ReLU 함수
ReLU 함수는 Rectified Linear Unit의 줄임말으로, 아래와 같은 식을 따른다.
\[f(z) = max(0, z)\]1
2
def relu(x):
return np.maximum(0, x)
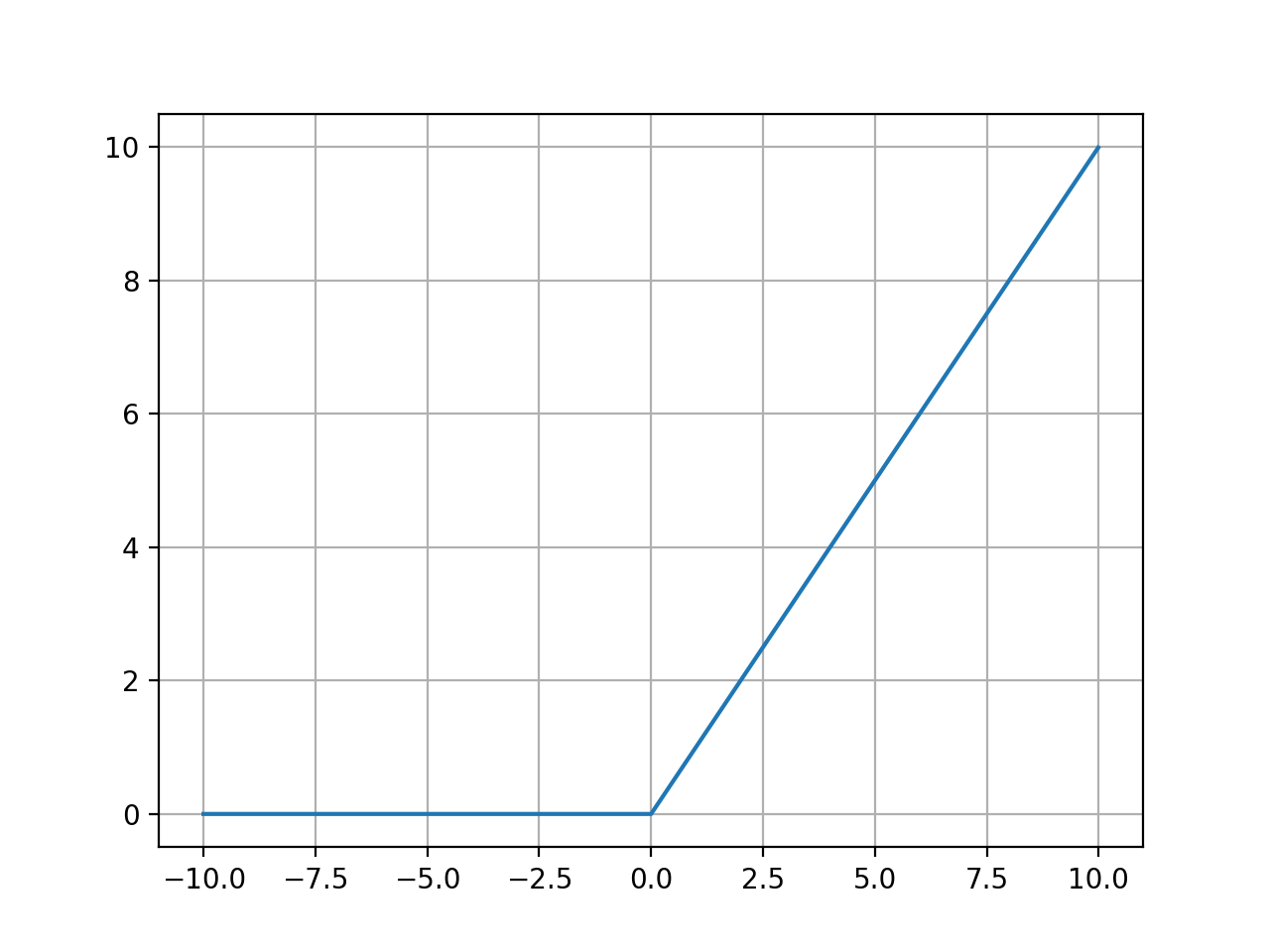
ReLU 함수는 0과 z 중 큰 값을 출력으로 삼는데, 이에 따라 입력 z가 음수일 경우에는 0이 출력되고 양수인 입력은 그대로 출력된다. Sigmoid 함수가 가장 먼저 등장했으나, 현재는 ReLU 함수가 가장 많이 사용된다.
Tanh 함수
\[f(z) = \frac{e^z - e^{-z}}{e^z + e^{-z}}\]1
2
def tanh(x):
return np.tanh(x) # nupmy 패키지 내에 tanh 함수가 정의되어 있음
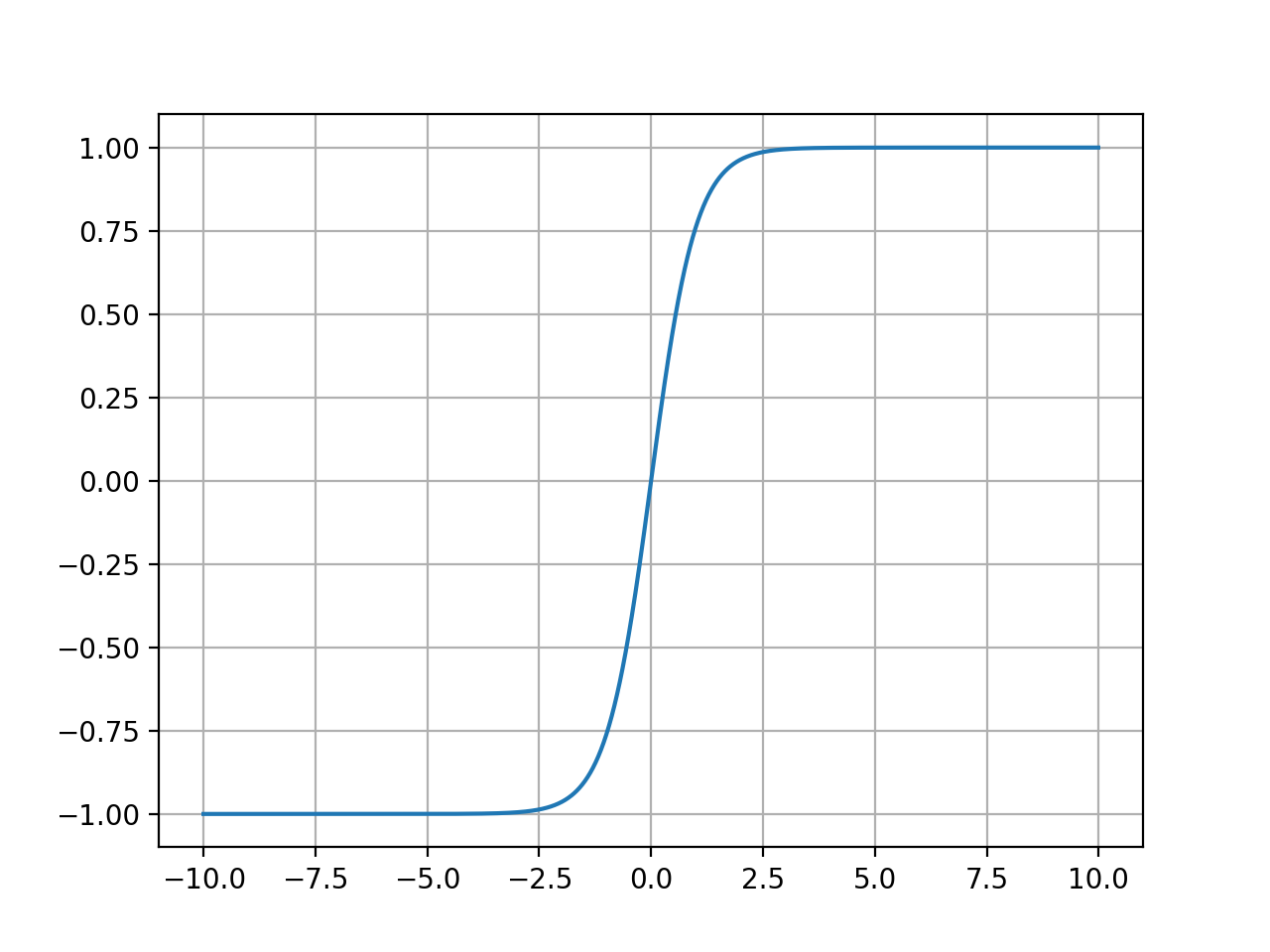
전체적으로 Sigmoid 함수와 유사한 형상을 가지고 있지만, 출력이 (0, 1)이 아니라 (-1, 1)으로 정의되며 중간값은 0이다.
또한 Tanh 함수는 Sigmoid 함수와 다음과 같은 관계를 가지고 있다. \(tanh(x) = 2\sigma(2x)-1\)
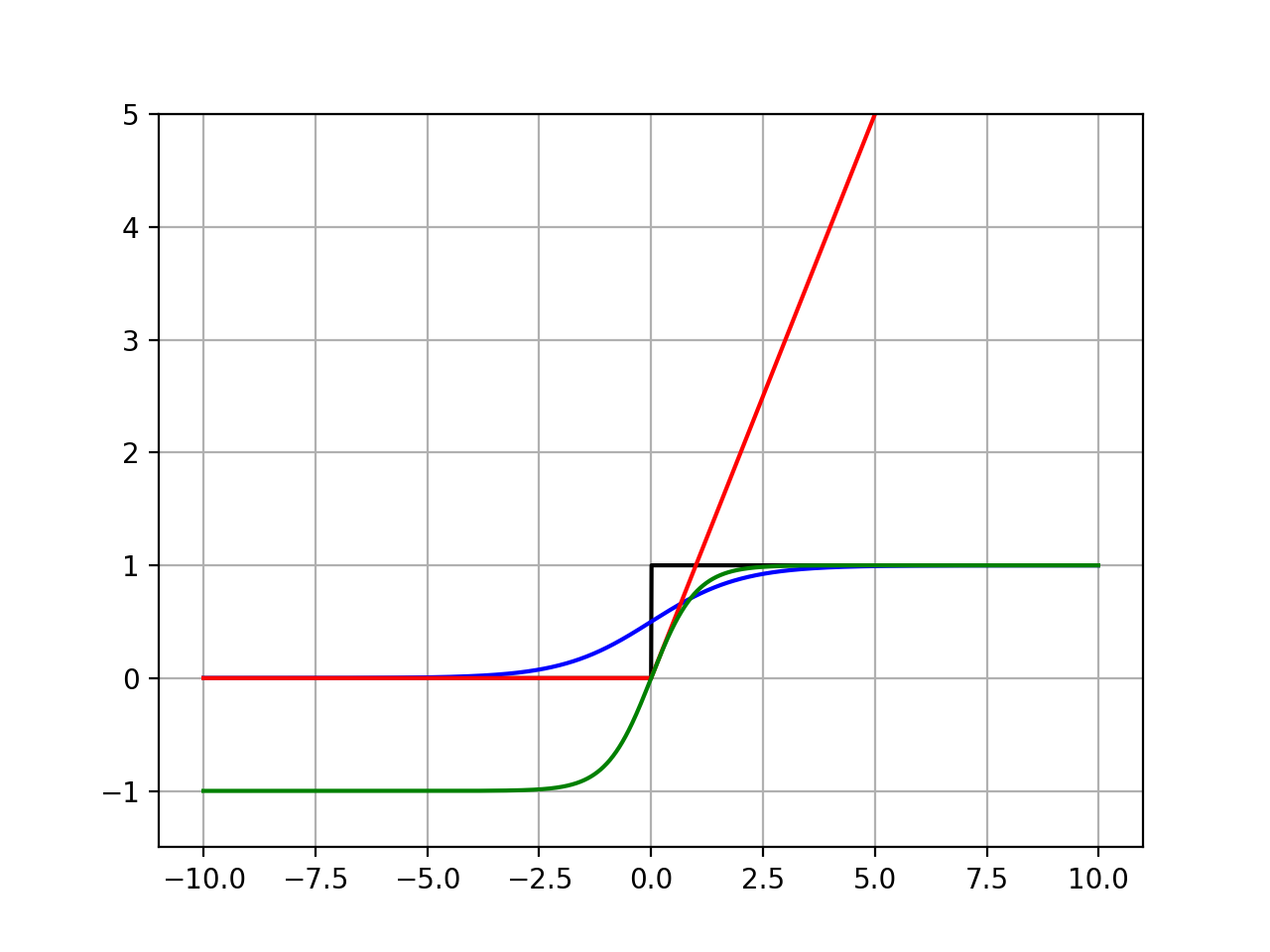
Activation 함수끼리 비교
지금까지 언급된 Activation 함수를 한번에 그려서 비교해 보는 코드를 작성해 보았다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
import numpy as np
import matplotlib.pyplot as plt
def threshold_function(x, threshold=0):
return np.array(x>threshold, dtype=np.int32)
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def relu(x):
return np.maximum(0, x)
def tanh(x):
return np.tanh(x)
x = np.arange(-10, 10, 0.01)
y0 = threshold_function(x)
y1 = sigmoid(x)
y2 = relu(x)
y3 = tanh(x)
plt.plot(x, y0, color='black')
plt.plot(x, y1, color='blue')
plt.plot(x, y2, color='red')
plt.plot(x, y3, color='green')
plt.ylim([-1.5, 5])
plt.grid(True)
plt.show()
Softmax 함수
Softmax 함수는 지금까지 언급했던 함수들과 약간 차이점이 있어 따로 설명한다.
\[y_k = \frac{exp(a_k)}{\sum_{i=1}^nexp(a_i)}\]1
2
def softmax(a):
return np.exp(a) / np.sum(np.exp(a))
이 함수는 여러개의 입력을 받고, 여러개의 출력을 낸다. 각각의 출력은 (0, 1) 사이로 제한되어 있으며, 출력을 모두 합하면 1이 된다.
이 특징에 따라서, Softmax 함수의 출력은 Sigmoid 함수와 마찬가지로 입력에 따른 출력의 확률로 해석할 수 있다. 아래 예시를 확인해보자. 입력이 큰 값일수록, 출력 역시 크다.
1
2
3
4
5
6
7
8
import numpy as np
def softmax(a):
return np.exp(a) / np.sum(np.exp(a))
input_a = np.array([-3, -1.5, 0.3, 0.6, 1, 1.8, 3])
print(np.round(softmax(input_a), 3))
실행 결과
[0.002 0.007 0.042 0.056 0.084 0.187 0.622]
Sigmoid 함수가 단일 사건의 발생 확률 (아까 키에 따라 대상이 남성일, 혹은 아닐 확률을 예시로 들었다)을 다루는 것과 달리 Softmax 함수는 주어진 여러개의 입력을 통해 각 사건의 발생 확률을 계산해낸다.
위에서 실행한 코드는 총 7개의 입력이 한꺼번에 주어졌는데, 이 입력들을 바탕으로 각각의 사건이 일어날 확률을 계산해내는 것이다. 주어진 입력 중 마지막 7번째 입력이 3으로 가장 크기 때문에, 마지막 출력이 0.622로 가장 크다. 분류 문제일 경우에는 이 데이터는 7번째 항목에 속할 확률이 62.2%라고 해석할 수 있겠다.
이 함수는 주로 분류 문제에 많이 사용된다. 예를 들어, 주어진 이미지가 강아지/고양이/호랑이/사람 중 어떤 것인지 분류하는 신경망의 마지막 출력 계층에 사용된다.
그 외 기타 Activation 함수
Linear/Identity
\[f(z) = z\]입력이 그대로 출력으로 나간다.
Softplus
\[f(z) = ln(1+exp(z))\]Leaky ReLU
\[f(z) = max(0.01z, z)\]ReLU를 약간 변형시킨 함수. 양수일 경우에는 z, 음수일 경우에는 0.01z가 출력된다.
Sigmoid 함수를 이용한 퍼셉트론
기존의 Threshold 대신, Sigmoid 함수를 Activation으로 적용한 새로운 퍼셉트론의 코드를 작성해 보았다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
import numpy as np
import matplotlib.pyplot as plt
def sigmoid(x):
return 1 / (1 + np.exp(-x))
class Perceptron:
def __init__(self, w, bias=-0.5):
self.weight = w
self.bias = bias
def affine(self, x):
self.sum = np.sum(self.weight * x) + self.bias
return self.sum
def activation(self):
# Sigmoid activation
return sigmoid(self.sum)
def work(self, x):
self.affine(x)
return self.activation()
draw_x = np.linspace(-5.0, 5.0, 1000)
draw_y = sigmoid(draw_x)
x = np.array([
[-3, -1, -2],
[0.3, 0.4, -0.5],
[-0.4, 0.2, 0.7],
[0.1, 0.5, 0.9],
[0.6, 0.7, 0.9],
[1.2, 0.4, 1.5],
[2, 2, 2]
])
w = np.array([0.3, 0.2, 0.5])
neuron = Perceptron(w)
plt.plot(draw_x, draw_y)
for each_x in x:
affine_point = np.round(neuron.affine(each_x), 3)
point_y = np.round(neuron.work(each_x), 3)
print(str(each_x) + " -> " + str(affine_point) + " -> " + str(point_y))
plt.scatter(affine_point, point_y, color='red')
plt.ylim([-0.5, 1.5])
plt.grid(True)
plt.show()
실행 결과
[-3. -1. -2.] -> -2.6 -> 0.069
[ 0.3 0.4 -0.5] -> -0.58 -> 0.359
[-0.4 0.2 0.7] -> -0.23 -> 0.443
[0.1 0.5 0.9] -> 0.08 -> 0.52
[0.6 0.7 0.9] -> 0.27 -> 0.567
[1.2 0.4 1.5] -> 0.69 -> 0.666
[2. 2. 2.] -> 1.5 -> 0.818
입력에 따른 Affine의 수치에 따라 앞의 Sigmoid 그래프에서 확인했던 것과 같은 출력값을 내놓는 것을 볼 수 있다. 이를 그림으로 확인하면 아래와 같다.
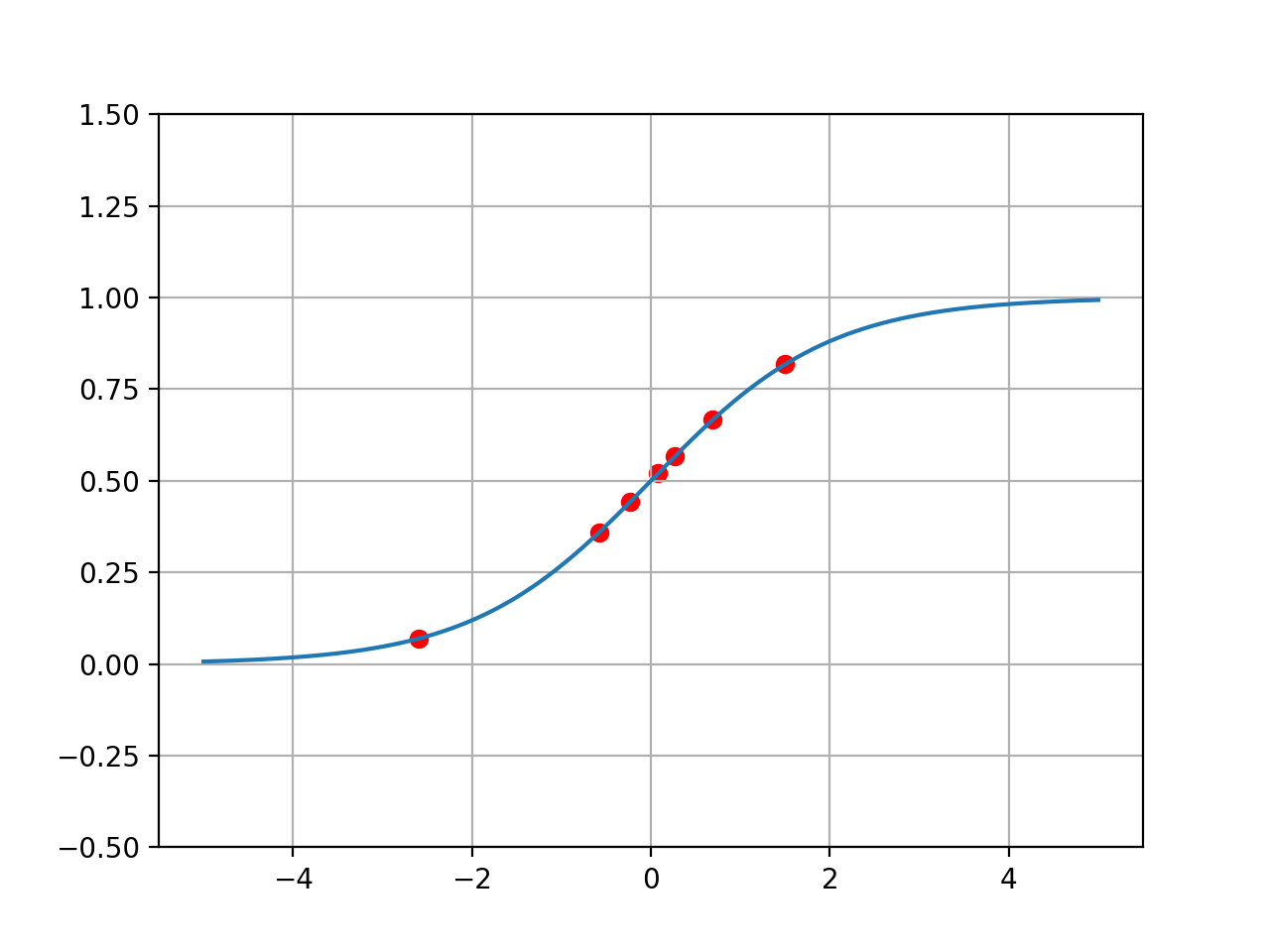
결론
지금까지 퍼셉트론에 Threshold 함수를 이용하는 것으로는 충분하지 않은 경우가 있다는 것을 확인했고, 그 대안으로서 Sigmoid, Relu, Tanh 등 다른 Activation 함수에 대해서 알아보았다. 이런 Activation 함수는 미분 가능하다는 특징이 있는데, 이는 나중에 학습을 위해서 중요한 요소이다.