개요
미분의 기본 개념을 간단하게 정리하고, 도함수를 컴퓨터를 이용해서 구하는 방법을 알아본다.
미분
관찰하기
파이썬을 통해서 y = x^3의 그래프를 그려 보았다.
1
2
3
4
5
6
7
8
9
10
11
12
import numpy as np
import matplotlib.pyplot as plt
def func(x):
return x**3
x = np.linspace(-5, 5, 100)
plt.plot(x, func(x)) # Basic graph
plt.grid()
plt.show()
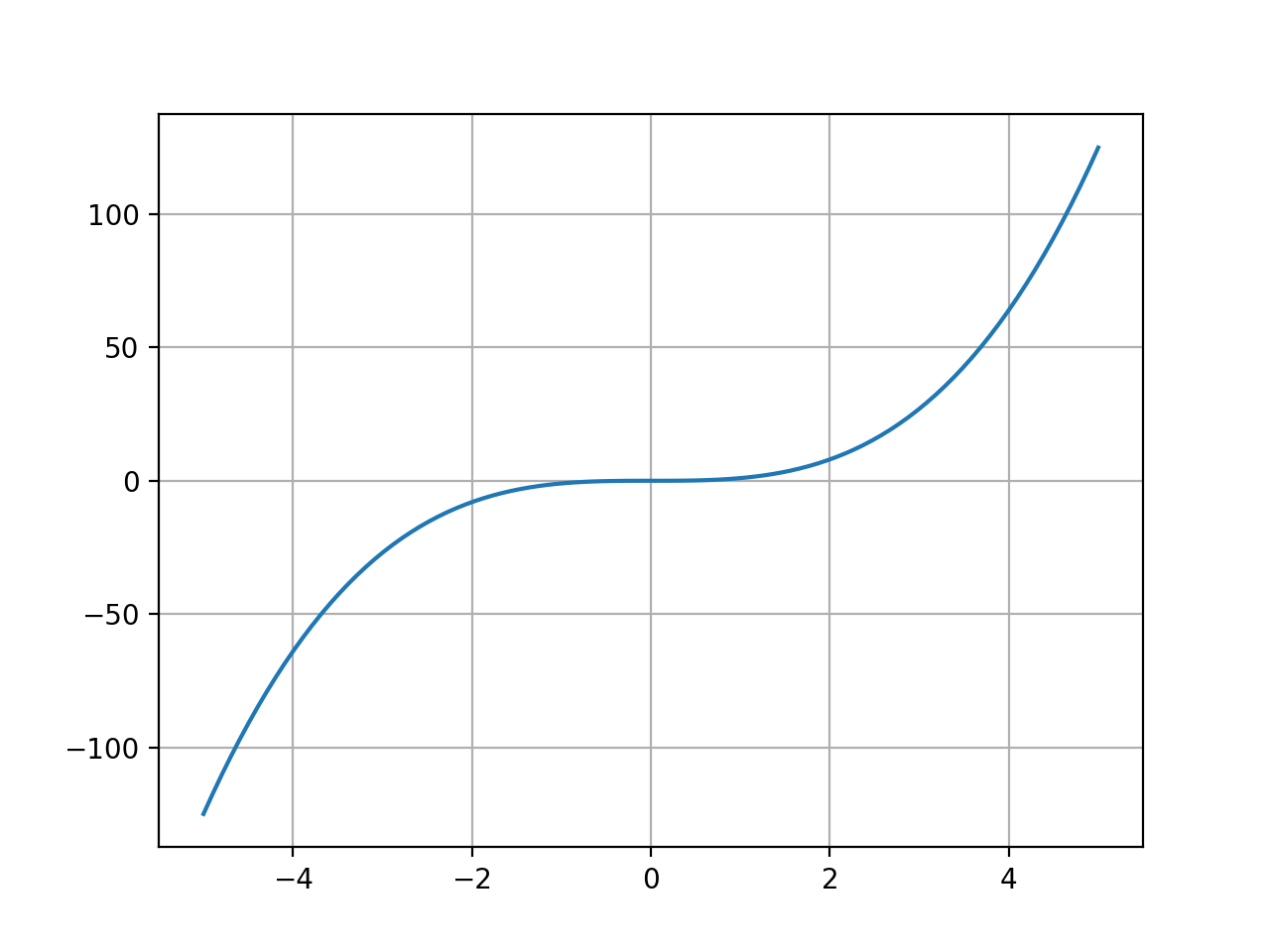
그래프를 보면 0 근처에서는 평평하고, 끝부분에서는 가파르다. 방금 ‘평평하다’ ‘가파르다’ 라는 표현을 사용했는데, 여기에 대해서 조금 더 자세히 파헤쳐보자.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
import numpy as np
import matplotlib.pyplot as plt
def func(x):
return x**3
x = np.linspace(-5, 5, 100)
plt.plot(x, func(x)) # Basic graph
plt.plot([2, 5], [func(2), func(5)], linestyle='--', color='gray') # Tangent
plt.plot([2, 4], [func(2), func(4)], linestyle='--', color='gray')
plt.plot([2, 3], [func(2), func(3)], linestyle='--', color='red')
plt.plot([2, 1], [func(2), func(1)], linestyle='--', color='red')
plt.plot([2, -4], [func(2), func(-4)], linestyle='--', color='gray')
plt.grid()
plt.show()
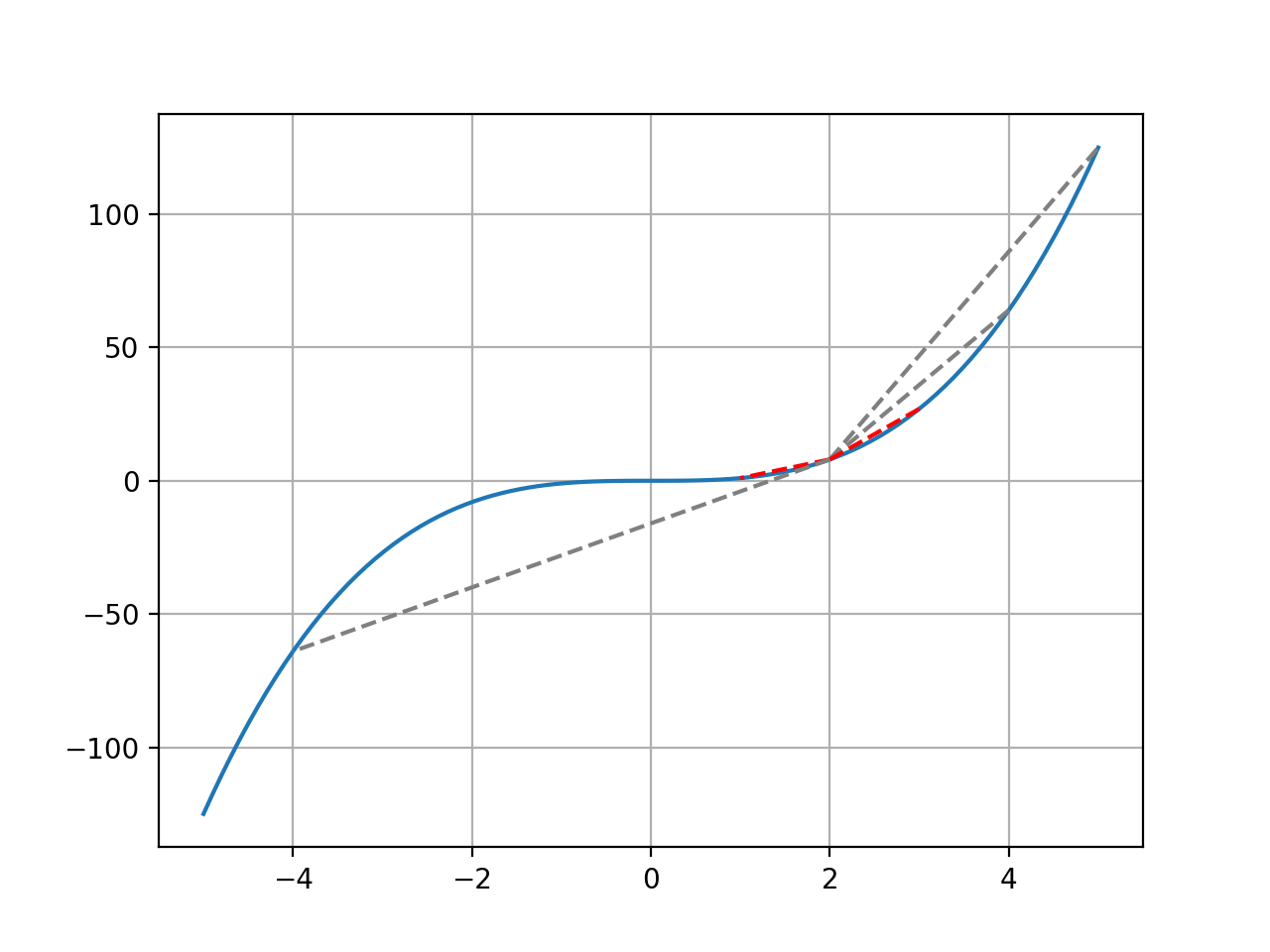
2를 중심으로, 함수 그래프 상의 몇몇 점과 직선을 그어 보았다.
2와 5 사이의 직선을 보면 x축 상의 거리는 3인데, y축 상의 함수값 변화는 크기 때문에 가파른(기울기가 큰) 직선이 그어졌다.
한편 2와 -4 사이의 직선은 x축 상의 거리가 6으로 앞서 언급한 직선의 2배이지만, 상대적으로 y축 함수값의 변화가 작았기에 기울기가 상대적으로 작은 직선이 그어졌다.
즉 이 직선들은 x축의 거리, 곧 변화량과 y축의 변화량 간의 관계를 나타낸다!
\[m = \frac{\Delta{y}}{\Delta{x}} = \frac{|f(x_2)- f(x_1)|}{|x_2 - x_1|}\]자세히 관찰하기
관찰 결과를 바탕으로, 위 그래프에서 2 주변에 돋보기를 대 보자.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
import numpy as np
import matplotlib.pyplot as plt
def func(x):
return x**3
x = np.linspace(1, 3, 100)
plt.plot(x, func(x)) # Basic graph
plt.plot([2, 2.5], [func(2), func(2.5)], linestyle='--', color='gray')
plt.plot([2, 1.2], [func(2), func(1.2)], linestyle='--', color='gray')
plt.plot([2, 2.1], [func(2), func(2.1)], linestyle='--', color='red')
plt.plot([2, 1.8], [func(2), func(1.8)], linestyle='--', color='blue')
plt.grid()
plt.show()
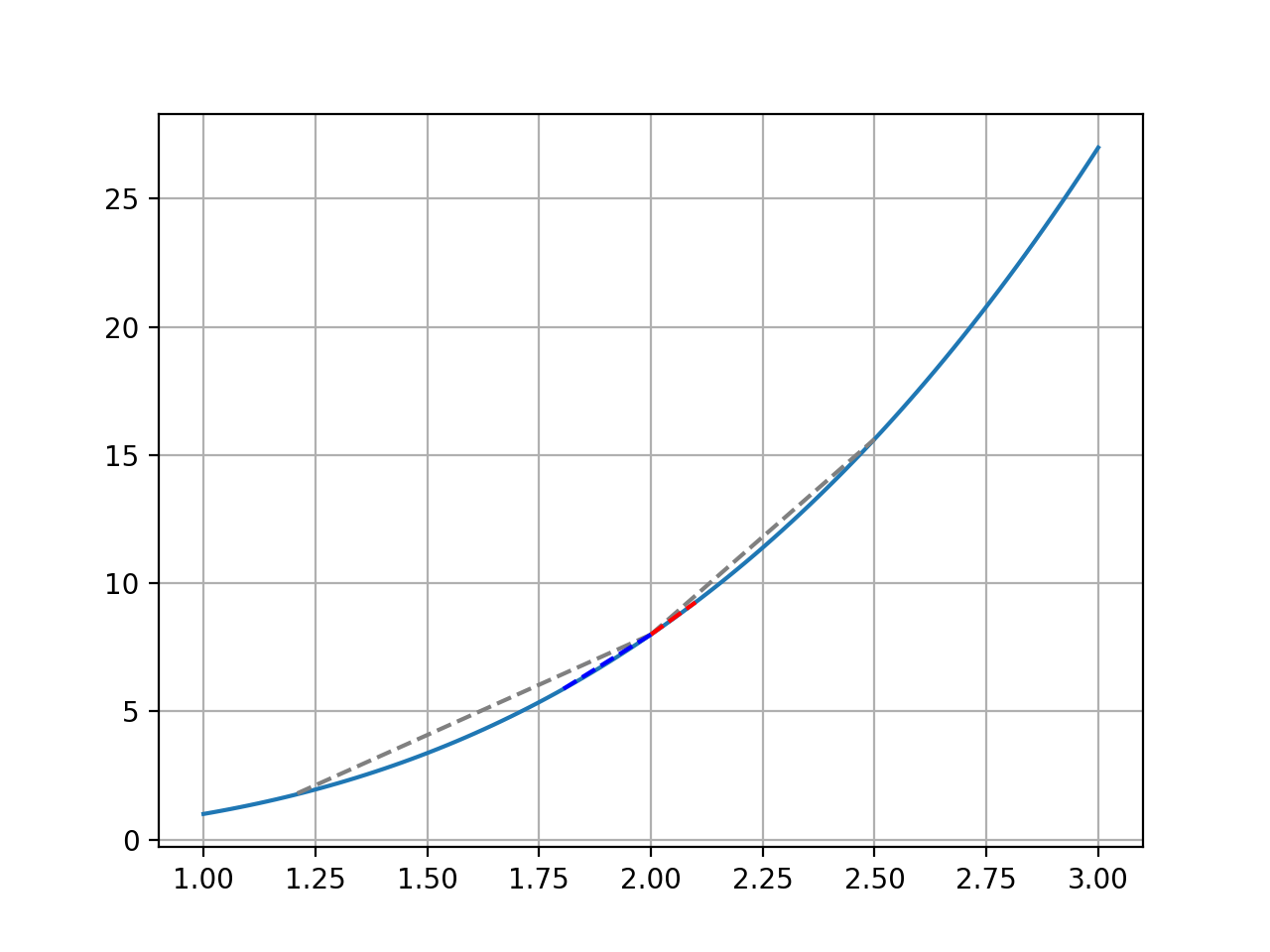
붉은 선과 푸른 선은 이제 거의 함수에 딱 붙은 직선이 되었다. 여기서 한번 더 자세히 보기로 하자.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
import numpy as np
import matplotlib.pyplot as plt
def func(x):
return x**3
def draw_line(x1, y1, x2, y2):
delta_x = abs(x2 - x1)
delta_y = abs(y2 - y1)
tangent = np.round(delta_y / delta_x, 3)
bias = y1 - tangent*x1
x = np.linspace(1, 3, 1000)
line = tangent*x + bias
plt.plot(x, line)
plt.text(2.1, 7.5, str(tangent))
x = np.linspace(1.5, 2.5, 100)
plt.plot(x, func(x)) # Basic graph
draw_line(2, func(2), 2.01, func(2.01))
plt.axis([1.5, 2.5, 0, 20])
plt.grid()
plt.show()
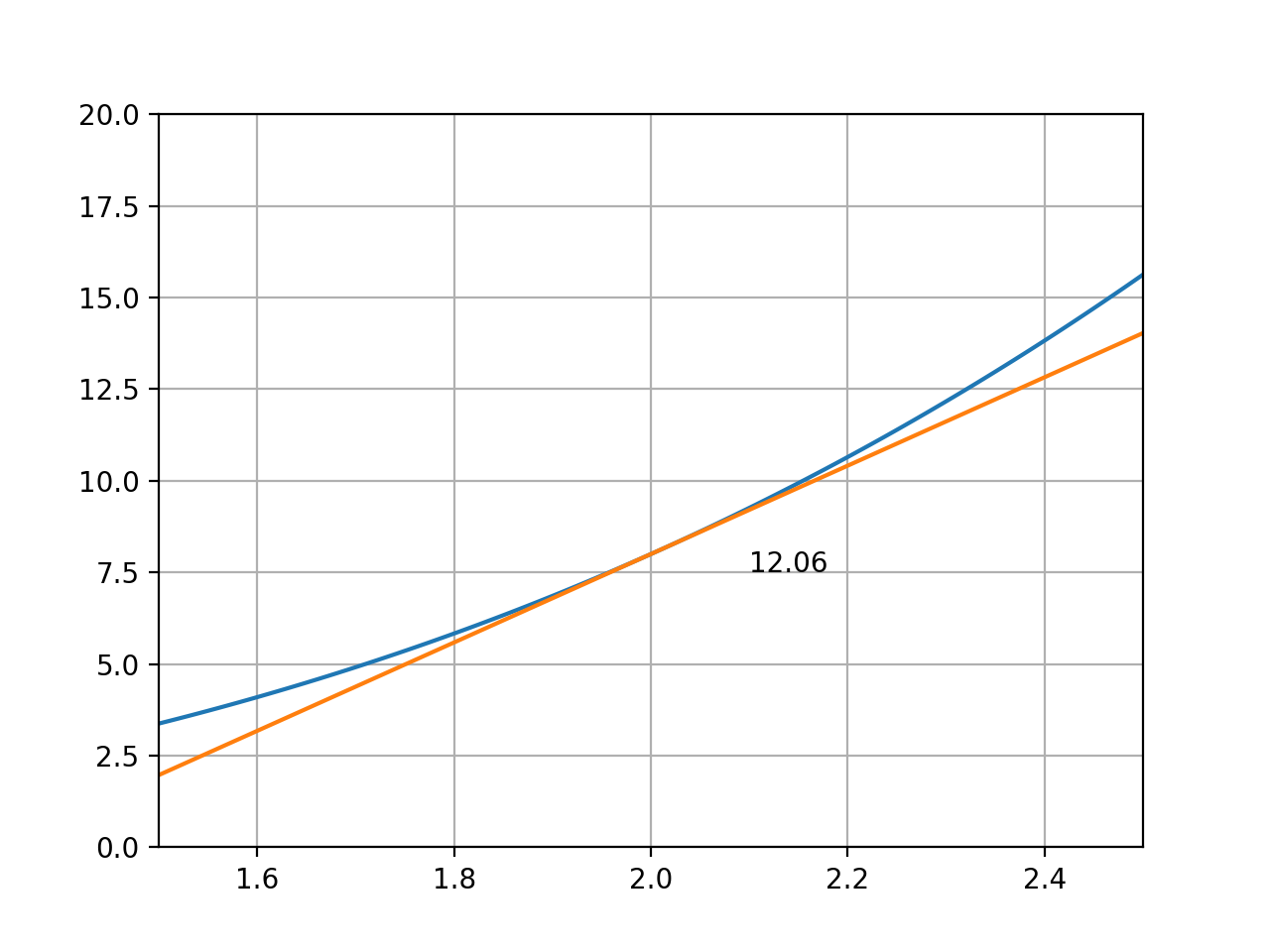12.06은 주황색 직선의 기울기 값이다.
이제 수학 책에서 보던 그림과 조금 더 비슷해졌다. 우리는 아주 짧은 구간 (지금은 2와 2.01)에 대한 기울기를 알아내었다. 그런데 이렇게 짧은 구간을 더욱 더 짧게 한다면? 즉 2와 2.000001 사이의 기울기라면? 이것이 바로 미분이다.
\[m = \lim_{h\rightarrow0}\frac{\Delta{y}}{\Delta{x}} = \lim_{h\rightarrow0}\frac{f(a+h)- f(a)}{h}\]2와 2.01을 잇는 주황색 직선은 2라는 지점에서 2.01까지 진행하는데 이정도 기울기(=빠르기)로 상승하고 있음을 보여준다. 기울기가 양수이기 때문에, 함수값이 커지고 있음을 의미한다.
도함수
우리는 방금 특정 지점, 2에서의 미분을 행했다. 만약에 미분을 주어진 함수의 모든 구간에서 행한다면? 그것이 바로 도함수 f’(x)이다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
import numpy as np
import matplotlib.pyplot as plt
def func(x):
return x**3
def analytic_derivative(x):
return 3*(x**2)
def numerical_derivative(x, h):
y = []
for each_x in x:
tangent = (func(each_x+h) - func(each_x)) / h
y.append(tangent)
return y
h = 1e-3 # = 0.001
x = np.arange(-5, 5, h)
plt.plot(x, func(x)) # Basic graph
plt.plot(x, analytic_derivative(x), color='green')
plt.plot(x, numerical_derivative(x, h), color='red')
plt.grid()
plt.show()
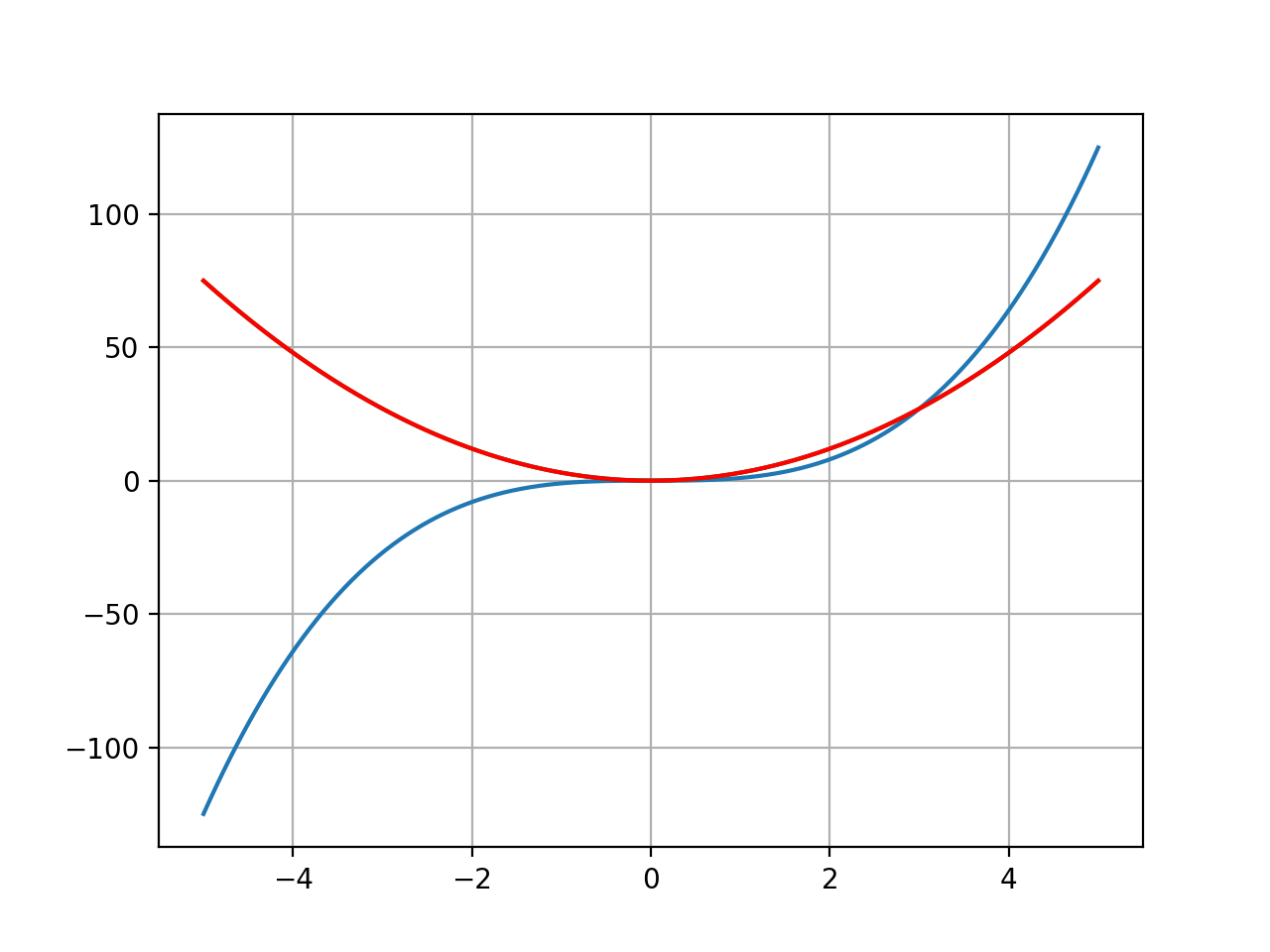
위에서 언급한 기울기를 구하는 공식을 이용해서, h = 0.001으로 가정하여 도함수를 구하고 그려 보았다. 녹색 선으로 우리가 알고 있는 x^3의 도함수인 3x^2를 그리도록 했는데, 붉은 선으로 이를 완전히 덮어버렸기 때문에 보이지 않는다. 즉 붉은 선과 녹색 선이 거의 같음을 알 수 있다!
물론 지금은 우리가 도함수가 무엇인지 알고 있는 상태에서 그것을 비교해 본 것이지만, 도함수를 모르는 상태에서도 같은 방식으로 컴퓨터를 이용해서 도함수를 구해낼 수 있다.
이런 기법을 수치해석이라고 하는데, 따로 학문 분야가 있을 정도로 깊이가 깊은 영역이다.
결론
미분, 결코 어려운 게 아니다! 그저 변화율을 의미할 뿐이다!