개요
함수의 극값의 개념에 대해 알아보고, 이것이 어떤 의미를 가지고 있는지 알아본다.
함수의 최소값 구하기
\[y = (x-1)(x+3) = x^2+2x - 3\]위와 같은 2차함수의 그래프를 그려보고, 그 최소값을 확인해 보자.
2차함수를 관찰하기
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
import numpy as np
import matplotlib.pyplot as plt
def func(x):
y = (x-1)*(x+3)
return y
def numerical_derivative1(x, h):
y = []
for each_x in x:
tangent = (func(each_x+h) - func(each_x)) / h
y.append(tangent)
return y
h = 1e-3 # = 0.001
x = np.arange(-5, 5, h)
line1, = plt.plot(x, func(x), label='Func') # Basic graph
line2, = plt.plot(x, numerical_derivative1(x, h), color='orange', label='1st Derivative')
plt.scatter(-3, 0, color='cornflowerblue')
plt.scatter(1, 0, color='cornflowerblue')
plt.scatter(-1, 0, color='orange')
plt.scatter(-1, -4, color='blue')
plt.plot([-1, -1], [0, -4], color='gray', linestyle='--')
plt.legend(handles=(line1, line2))
plt.grid()
plt.show()
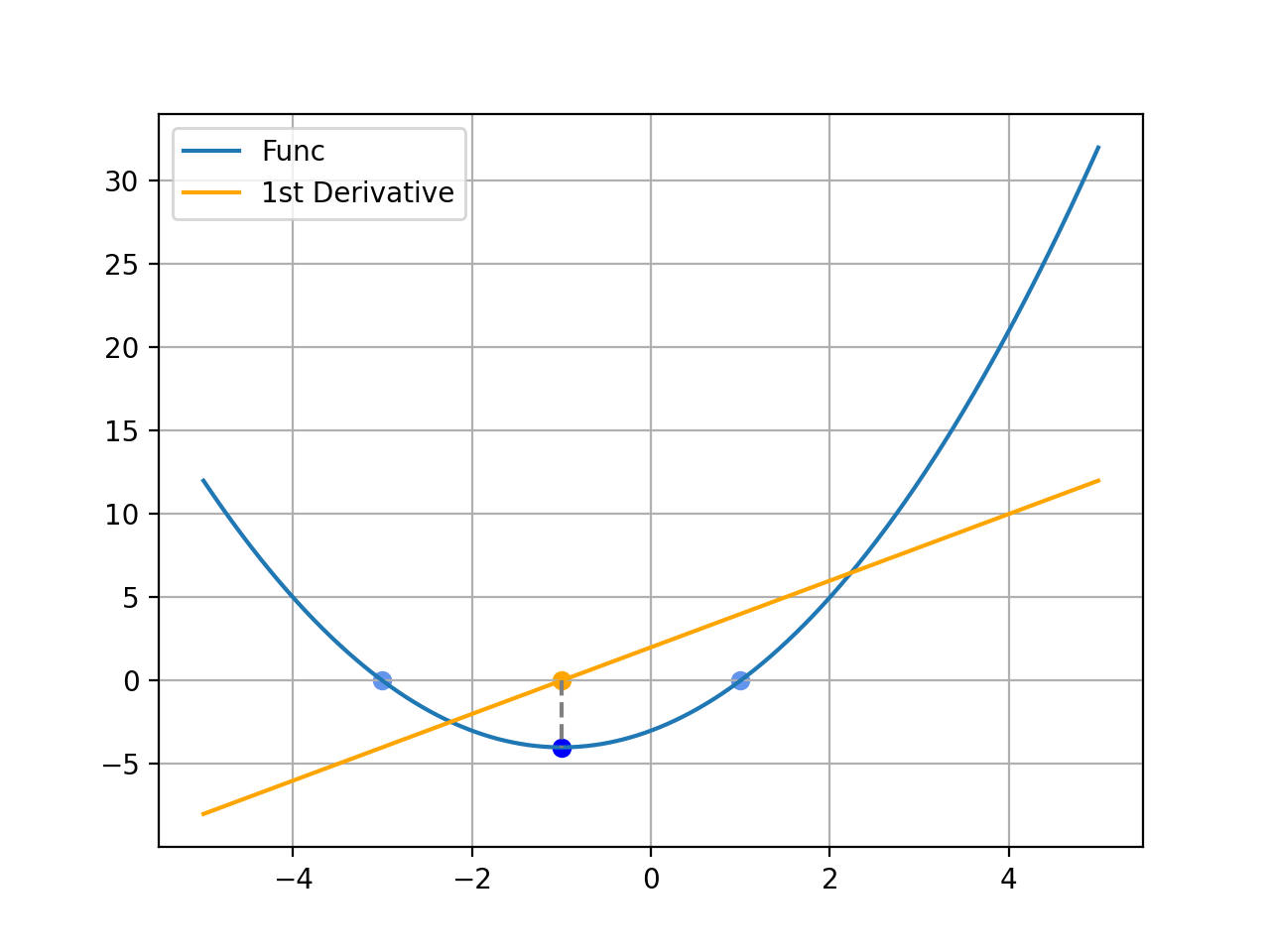
주어진 함수는 -3과 +1에서 근을 가지고, 그 최소값은 x=-1에서 y=-4로 주어진다. 한편 이 함수의 1차 도함수를 함께 그려보았다. 그 결과, 원래 함수의 도함수의 함수값이 0일 경우에 함수가 최소값을 가짐을 알 수 있다.
잠깐 생각해보면 직관적으로 바로 이해할 수 있다. 도함수의 함수값은 원래 함수가 그 지점에서 갖는 ‘변화율’을 의미하는데, 이 도함수가 0보다 작다면 함수가 감소하는 중이며, 0보다 크다면 함수가 증가하는 중인 것이다.
위와 같은 2차함수의 경우에는 처음에는 함수값이 감소했다가 증가하는 과정에서 기울기가 0, 즉 더 이상 함수값이 감소하지 않는 지점을 가지게 되는데 그 지점에서의 함수값이 바로 최소값인 것이다.
이는 2차함수의 최고차항이 음수여서 최대값을 가지는 경우에도 마찬가지로 적용된다.
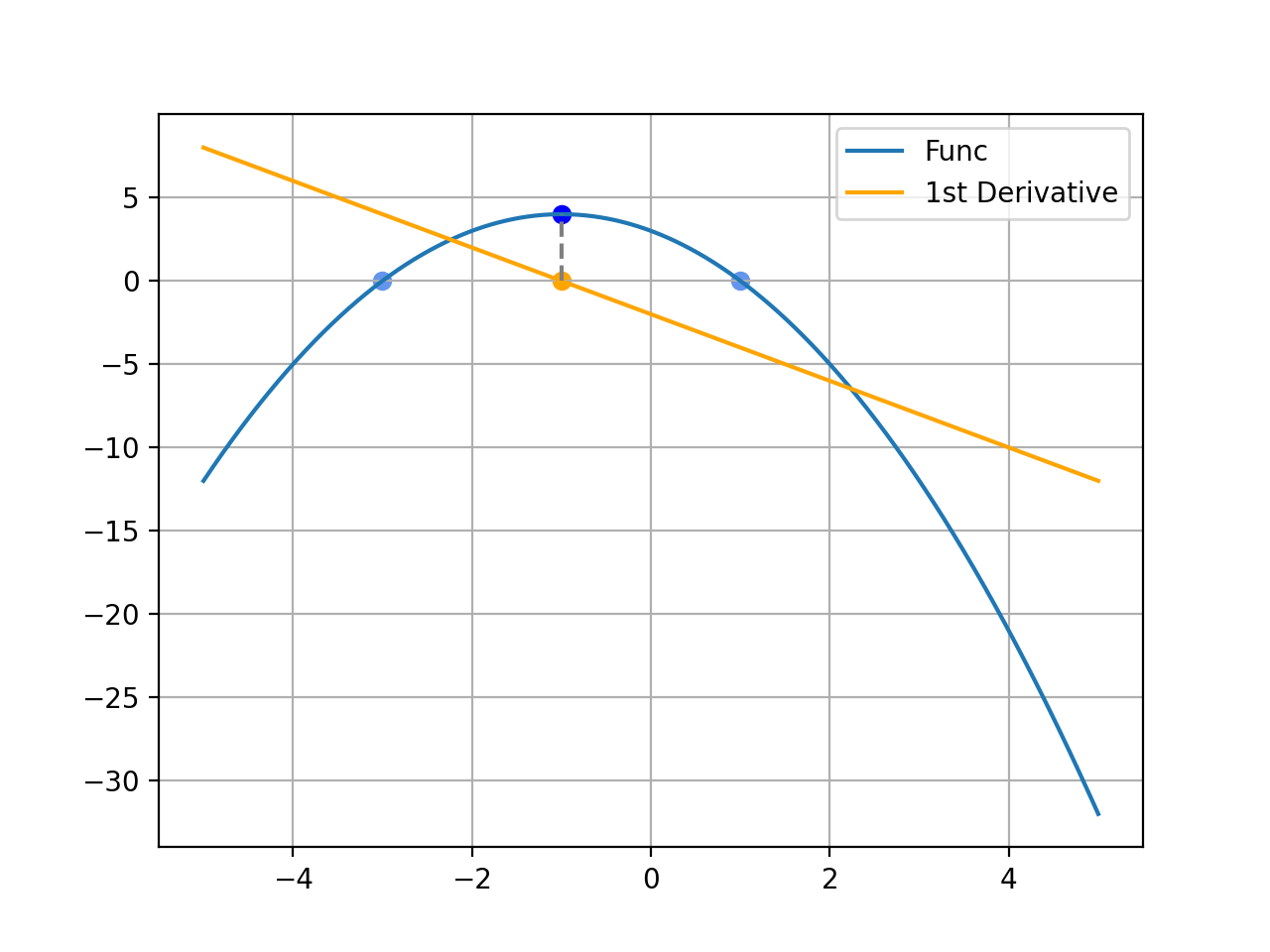
아까의 함수에 -1을 곱해 함수를 반대로 뒤집었다. 이때는 함수가 증가하다가 감소하는 형태를 띄기 때문에, 더 이상 함수값이 증가하지 않아서 기울기가 0이 되는 지점이 바로 최대값이 된다.
다른 함수의 경우
3차함수 Case 1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
import numpy as np
import matplotlib.pyplot as plt
def func(x):
y = (1/3)*(x**3) - 4*x
return y
def numerical_derivative1(x, h):
y = []
for each_x in x:
tangent = (func(each_x+h) - func(each_x)) / h
y.append(tangent)
return y
h = 1e-3 # = 0.001
x = np.arange(-5, 5, h)
line1, = plt.plot(x, func(x), label='Func') # Basic graph
line2, = plt.plot(x, numerical_derivative1(x, h), color='orange', label='1st Derivative')
plt.scatter(-5, func(-5), color='red')
plt.scatter(5, func(5), color='red')
plt.scatter(-2, func(-2), color='blue')
plt.scatter(2, func(2), color='blue')
plt.scatter(-2, 0, color='orange')
plt.scatter(2, 0, color='orange')
plt.plot([-2, -2], [0, func(-2)], color='gray', linestyle='--')
plt.plot([2, 2], [0, func(2)], color='gray', linestyle='--')
plt.legend(handles=(line1, line2))
plt.grid()
plt.show()
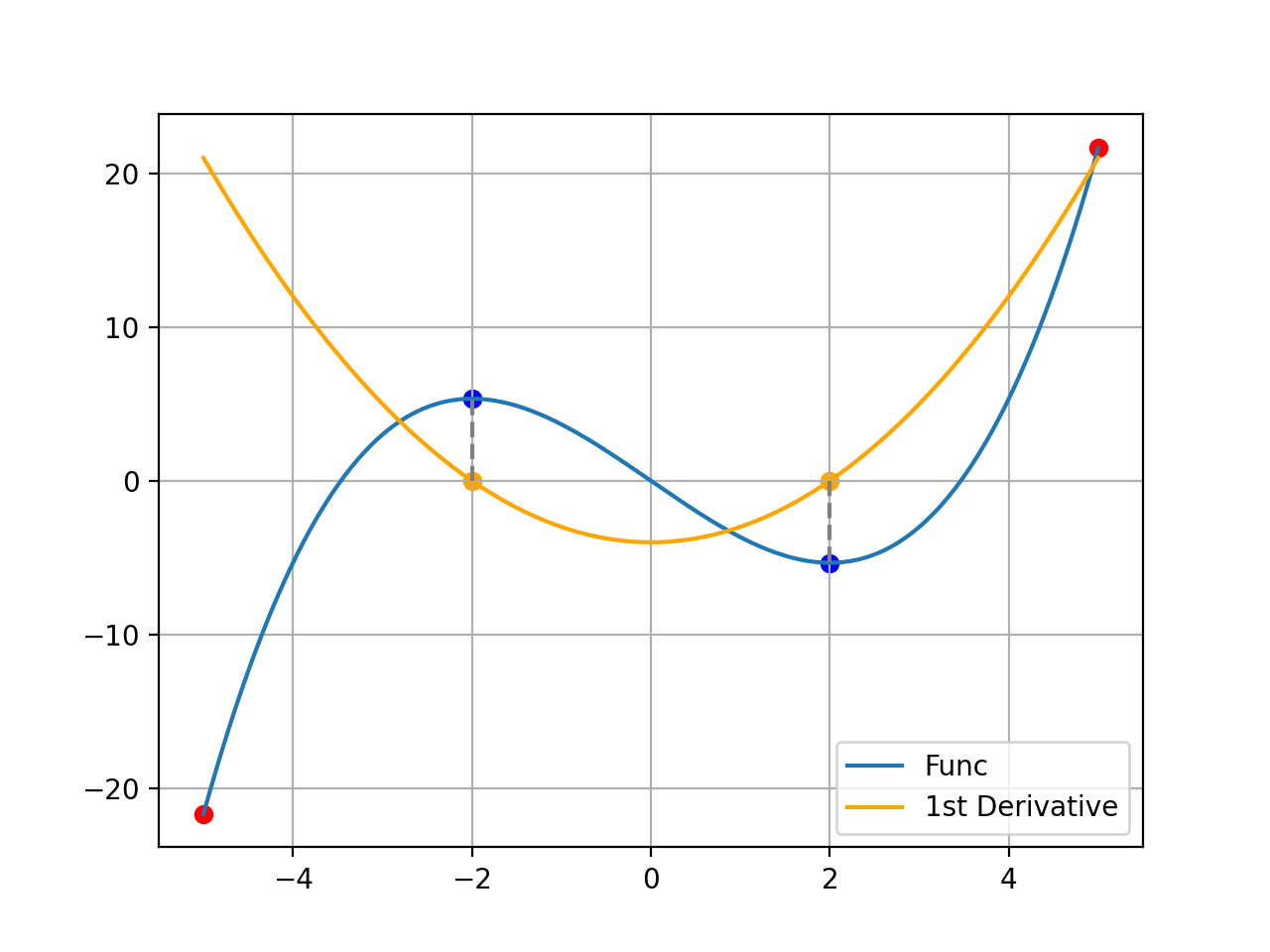
3차 함수를 그려 보았다. 이 함수는 도함수로 y = (x-2)(x+2)를 가지기 때문에, -2와 +2에서 최대값과 최소값… 이 아니라 극대값과 극소값을 가진다. 이 3차함수는 [-5, 5] 구간 내에서 -5일때 최소값, +5일때 최대값을 가진다. 이를 붉은 점으로 표시했다.
- 최대값: 주어진 구간에서 가장 큰 값
- 최소값: 주어진 구간에서 가장 작은 값
- 극대값: 그 주변에서 가장 큰 값
- 극소값: 그 주변에서 가장 작은 값
아까 2차함수의 사례에서 보았듯이 최대값과 최소값은 각각 극대값과 극소값에도 해당하지만, 이 3차함수의 경우에서도 볼 수 있듯이 그 반대는 성립하지 않는다.
3차함수 Case 2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
import numpy as np
import matplotlib.pyplot as plt
def func(x):
y = (x-2)**3
return y
def numerical_derivative1(x, h):
y = []
for each_x in x:
tangent = (func(each_x+h) - func(each_x)) / h
y.append(tangent)
return y
h = 1e-3 # = 0.001
x = np.arange(-5, 10, h)
line1, = plt.plot(x, func(x), label='Func') # Basic graph
line2, = plt.plot(x, numerical_derivative1(x, h), color='orange', label='1st Derivative')
plt.scatter(-5, func(-5), color='red')
plt.scatter(10, func(10), color='red')
plt.scatter(2, 0, color='orange')
plt.legend(handles=(line1, line2))
plt.grid()
plt.show()
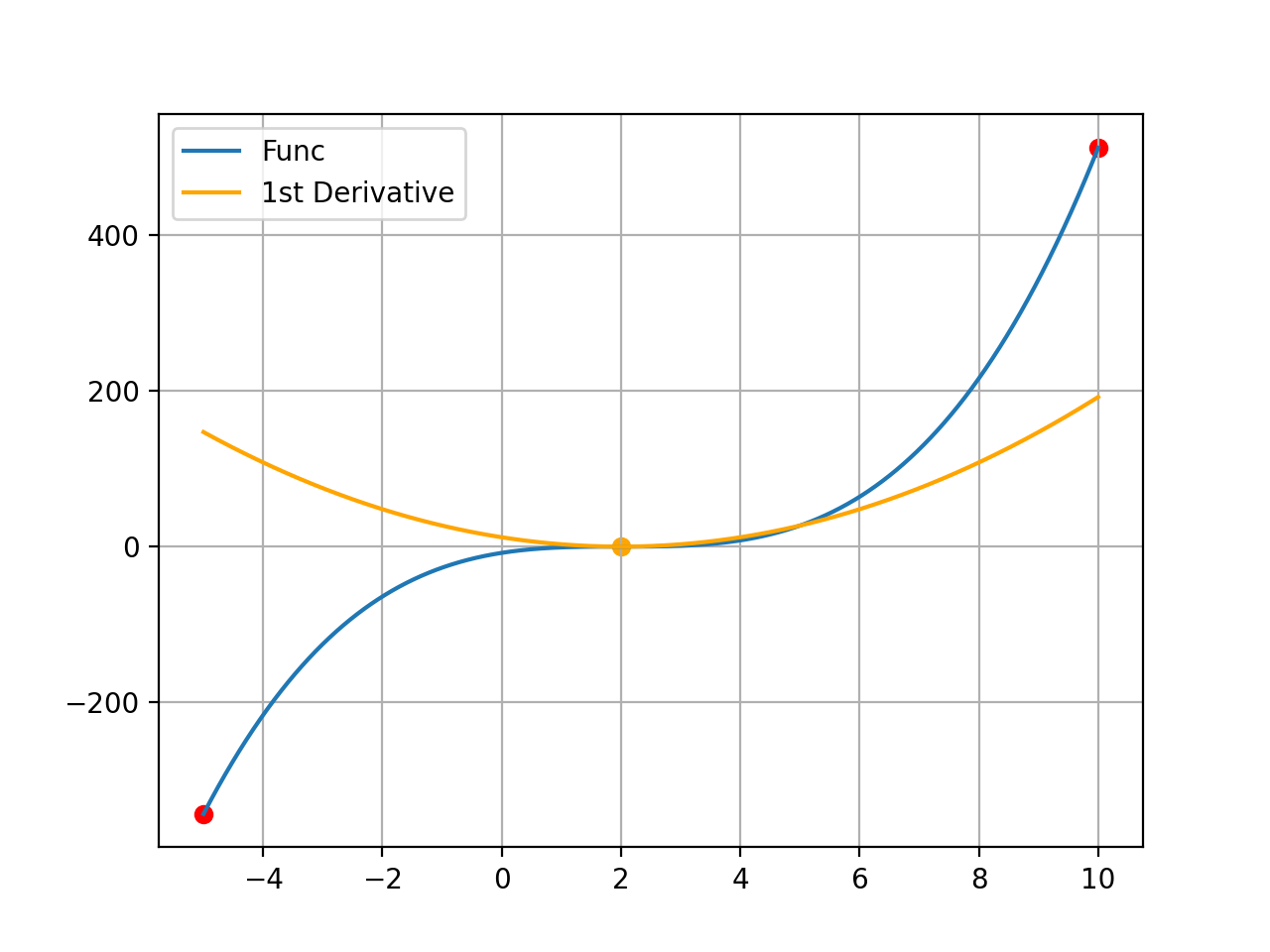
이 함수의 경우에는 x=2에서 도함수 f’(x)=0인데도 이 점이 극대값과 극소값 어느 쪽에도 해당하지 않는다. 잘 살펴보면 2차함수 꼴을 가지는 f’(x)가 0을 지난 뒤 다시 양수 구간을 가지기 때문에, 이 점에서 잠깐 증가를 멈추었다가 계속 증가하는 모습을 보인다. 즉, 도함수의 함수값이 0이라고 해서 그 점이 꼭 극값을 가진다는 의미는 아니다.
이계 도함수를 이용하기
우리는 지금까지 f’(x)를 이용해서 극값을 찾으려고 해 보았는데, 이 과정에서 몇가지 문제에 봉착했다.
- 극대값과 극소값을 어떻게 구분할까?
- 극소값이 아니라 진짜 최소값을 찾는 방법은 무엇일까?
- 어떤 함수의 경우에는 f’(x)=0임에도 극값이 아닌 경우도 있는데, 어떻게 해야 할까?
이 문제를 해결하기 위해서, 이계 도함수 f’‘(x)를 이용해 보자.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
import numpy as np
import matplotlib.pyplot as plt
def func(x):
y = (1/3)*(x**3) - 4*x
return y
def numerical_derivative1(x, h):
y = []
for each_x in x:
tangent = (func(each_x+h) - func(each_x)) / h
y.append(tangent)
return y
def numerical_derivative2(x, h):
d1 = numerical_derivative1(x, h)
y = []
for i in range(0, len(d1)-1):
tangent = (d1[i+1] - d1[i]) / h
y.append(tangent)
y.append(y[len(y)-1]) # 마지막꺼를 한번 더 복사,, 이게 최선일까?
return y
h = 1e-3 # = 0.001
x = np.arange(-5, 5, h)
line1, = plt.plot(x, func(x), label='Func') # Basic graph
line2, = plt.plot(x, numerical_derivative1(x, h), color='orange', label='1st Derivative')
line3, = plt.plot(x, numerical_derivative2(x, h), color='green', label='2nd Derivative')
plt.scatter(5, func(5), color='red')
plt.scatter(-5, func(-5), color='red')
plt.scatter(2, func(2), color='cornflowerblue')
plt.scatter(-2, func(-2), color='cornflowerblue')
plt.scatter(2, 0, color='orange')
plt.scatter(-2, 0, color='orange')
plt.scatter(2, 4, color='green')
plt.scatter(-2, -4, color='green')
plt.plot([2, 2], [func(2), 4], color='gray', linestyle='--')
plt.plot([-2, -2], [func(-2), -4], color='gray', linestyle='--')
plt.legend(handles=(line1, line2, line3))
plt.grid()
plt.show()
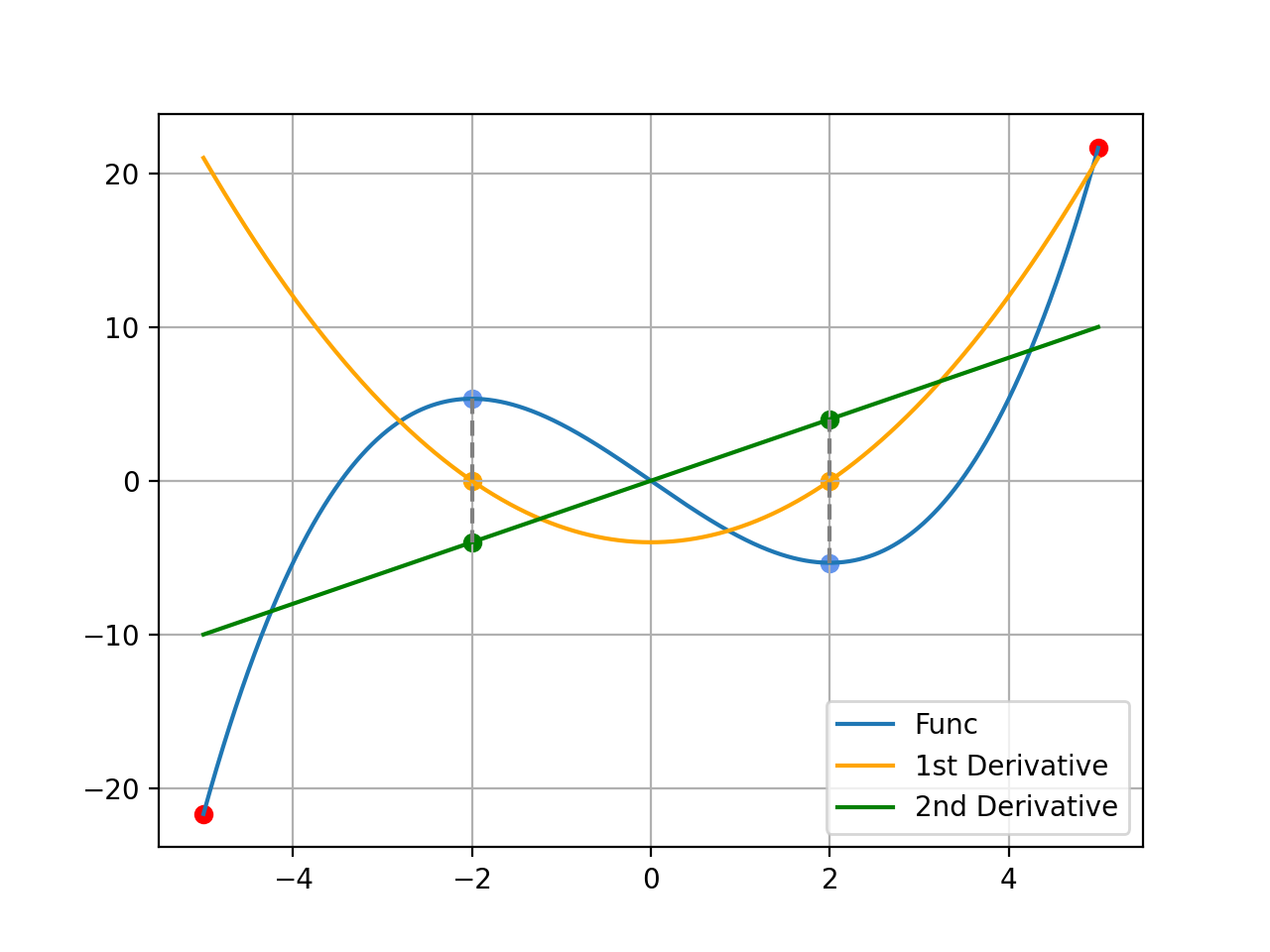
아까의 3차함수 그래프에 이계 도함수를 같이 그렸다. 이때 우리가 알 수 있는 사실은 일계 도함수의 함수값이 0인 지점에서 이계 도함수의 함수값이 음수일 때는 극대값, 반대로 양수일 때는 극소값을 가진다는 사실이다.
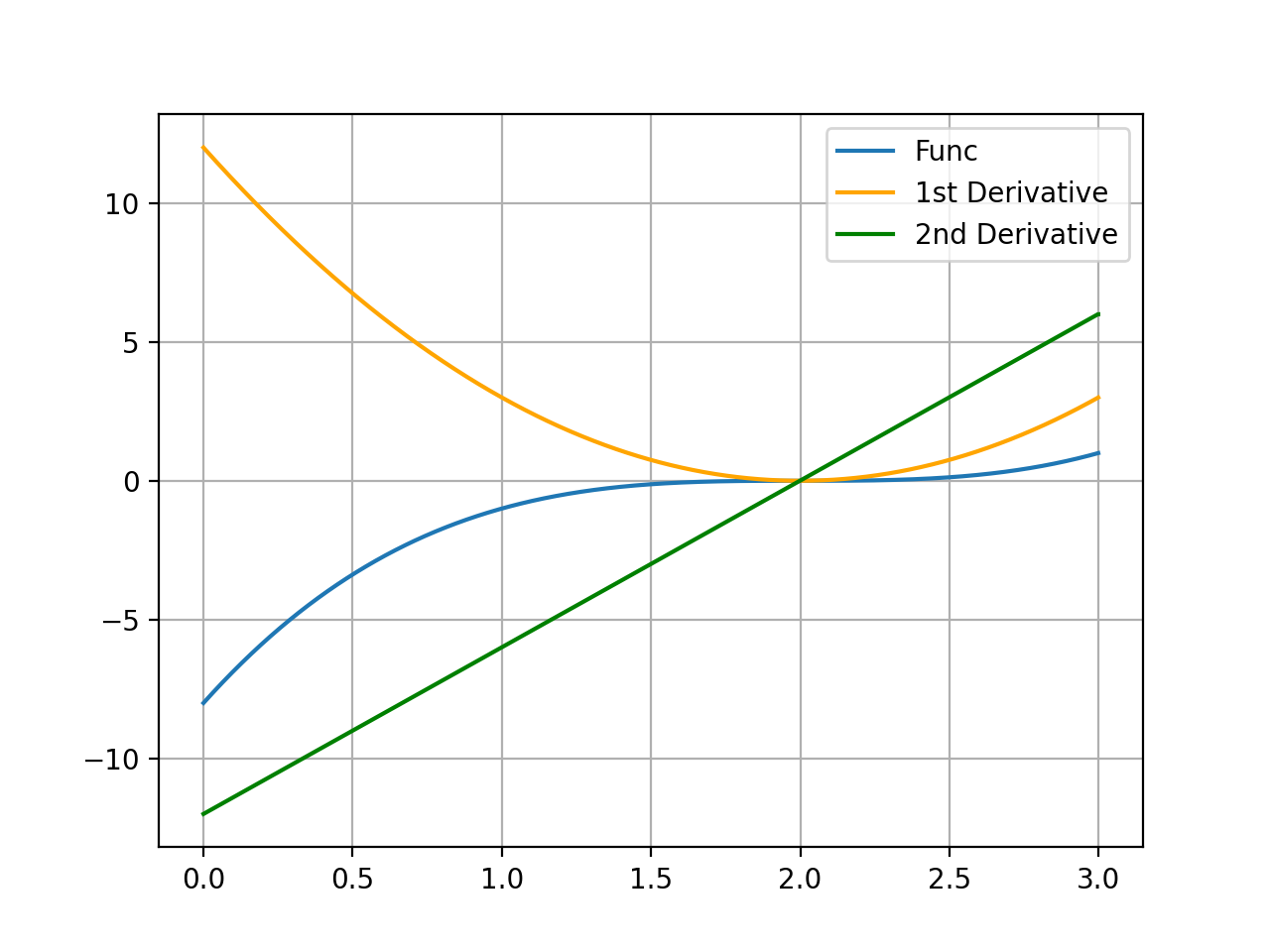아까 보았던 함수 중 x=2에서 일계 도함수의 함수값이 0이지만, 극점에 해당하지 않는 점이 있었다. 이때의 이계 도함수는 함수값이 0임을 확인할 수 있다. 즉, 일계 도함수와 이계 도함수의 함수값 모두 0인 지점은 극점이 아니다.
적용하기
지금까지 본 내용을 정리해서 함수의 최대값과 최소값을 다음과 같은 방법을 통해 찾을 수 있다.
- 주어진 함수 f(x)의 일계 도함수 f’(x)와 이계 도함수 f’‘(x)를 구한다.
- f’(x)=0을 충족하는 x들을 찾는다.
- 2의 조건을 충족하는 점에서 f’‘(x)의 함수값을 확인한다.
- f’‘(x) < 0일 경우, 이 점은 극대값을 가진다.
- f’‘(x) = 0일 경우, 이 점은 극점이 아니다.
- f’‘(x) > 0일 경우, 이 점은 극소값을 가진다.
- 한편, 주어진 함수의 구간 양쪽 끝이 극대값이나 극소값을 가지지 않는지 확인한다.
- 극대값 중 가장 큰 값이 최대값, 극소값 중 가장 작은 값이 최소값이다.
위와 같은 규칙을 가지고, y = sin(x)/x라는 함수에 대해서 (0, 4π] 구간에서 최대값과 최소값을 찾아보자.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
import numpy as np
import matplotlib.pyplot as plt
def func(x):
y = np.sin(x) / x
return y
def numerical_derivative1(x, h):
y = []
for each_x in x:
tangent = (func(each_x+h) - func(each_x)) / h
y.append(tangent)
return y
def numerical_derivative2(x, h):
d1 = numerical_derivative1(x, h)
y = []
for i in range(0, len(d1)-1):
tangent = (d1[i+1] - d1[i]) / h
y.append(tangent)
y.append(y[len(y)-1]) # 마지막꺼를 한번 더 복사,, 이게 최선일까?
return y
h = 1e-3 # = 0.001
PI = 3.141592
x = np.arange(0, 4*PI, h)
line1, = plt.plot(x, func(x), label='Func') # Basic graph
line2, = plt.plot(x, numerical_derivative1(x, h), color='orange', label='1st Derivative')
line3, = plt.plot(x, numerical_derivative2(x, h), color='green', label='2nd Derivative')
# f'(x) = (x cos(x) - sin(x))/x^2 = 0을 구했음.
plt.scatter(0, 0, color='orange')
plt.scatter(4.49, 0, color='orange')
plt.scatter(7.72, 0, color='orange')
plt.scatter(10.9, 0, color='orange')
plt.scatter(h, func(h), color='red') # / 0이 안되므로 h를 사용
plt.scatter(4.49, func(4.49), color='red')
plt.scatter(7.72, func(7.72), color='cornflowerblue')
plt.scatter(10.9, func(10.9), color='cornflowerblue')
plt.scatter(4*PI, func(4*PI), color='cornflowerblue')
plt.legend(handles=(line1, line2, line3))
plt.grid()
plt.show()
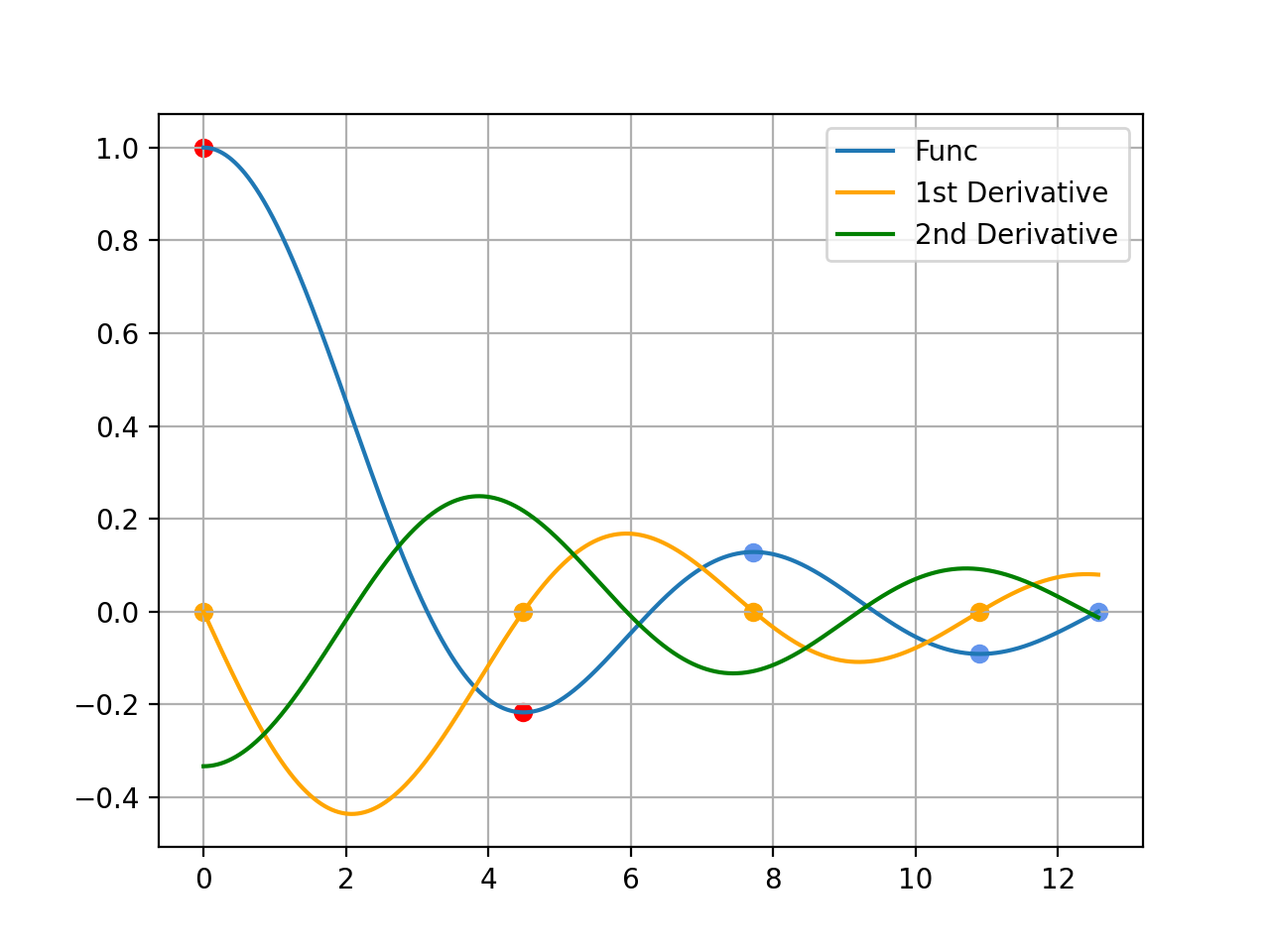
- 주어진 함수 f(x)의 일계 도함수 f’(x)와 이계 도함수 f’‘(x)를 구한다.
- f’(x)=0을 충족하는 x들을 찾는다. -> 0, 4.49, 7.72, 10.9
- 2의 조건을 충족하는 점에서 f’‘(x)의 함수값을 확인한다.
- f’‘(x) < 0일 경우, 이 점은 극대값을 가진다. -> f(0), f(7.72)
- f’‘(x) = 0일 경우, 이 점은 극점이 아니다. -> 해당사항 없음
- f’‘(x) > 0일 경우, 이 점은 극소값을 가진다. -> f(4.49), f(10.9)
- 한편, 주어진 함수의 구간 양쪽 끝이 극대값이나 극소값을 가지지 않는지 확인한다. -> 0, 4π에서 각각 극대값 f(0)과 극대값 f(4π)를 가짐
- 극대값 중 가장 큰 값이 최대값, 극소값 중 가장 작은 값이 최소값이다. -> 극대값 f(0), f(7.72), f(4π) 중 가장 큰 f(0)이 최대값이며, 극소값 f(4.49), f(10.9)중 가장 작은 f(4.49)가 최소값
의미
이렇게 일계 도함수와 이계 도함수를 이용해서 우리는 어떤 함수가 언제 최대값을 가지고, 또 최소값을 가지는지 알 수 있다.