개요
앞선 포스트에서 정의한 손실을 바탕으로, 어떻게 손실을 줄여서 신경망이 우리가 원하는 결과값을 도출할 수 있도록 학습시키는지 알아본다.
손실 줄이기
읽기 전에 시간이 있다면 함수의 최소값과 최대값에 대한 포스트을 확인해 보는 것이 좋다.
핵심을 간단히 요약하자면, 어떤 함수 f(x)에서 f’(x) = 0이고 f’‘(x) > 0인 점은 극소값을 가진다는 것이다. ‘손실을 줄인다’라는 우리의 목표는 손실 함수의 함수값을 최소화하는 것을 의미한다. 다시 말해서 손실 함수가 최소값을 갖는 지점을 찾는 것이다.
경사 하강법
그런데 항상 f’(x)=0이라는 수식을 풀어서 최소값을 찾을 수 있는 것은 아니다. 특히 매개변수가 여럿 있을 때 그런 경우가 발생할 수 있다. 이렇게 식을 풀어서 최소값을 갖는 지점을 찾을 수 없을 때는 경사 하강법을 이용할 수 있는데, 이에 대해서 알아보자. 경사 하강법은 말 그대로 경사를 따라 내려가는 방법이라고 할 수 있다
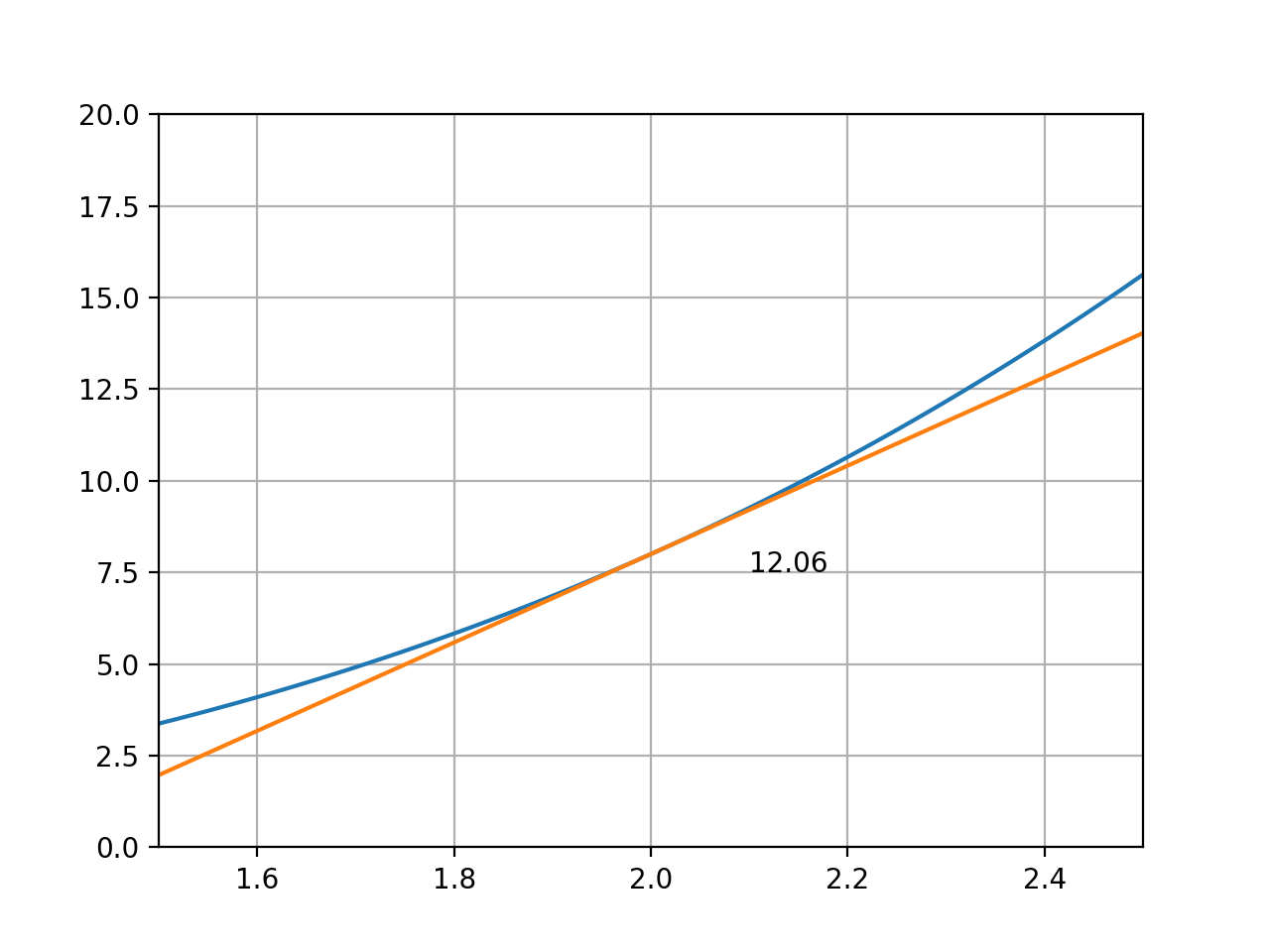
위 그림은 y=x^3에서 x=2와 x=2.01 사이의 기울기 직선을 확대하여 나타낸 것이다. 이때의 기울기 값이 12.06인데, 실제 f’(2)=12임을 감안하면 0.06의 오차가 있다. 그런데 이 값은 미분을 행할때 h=0.01을 기준으로 한 값이고, h=0.001이나 이보다 더 작은 값을 사용한다면 오차는 더욱 작아진다. f’(x) 전체를 구할 수 없을 때에도 이와 같은 방식으로 특정 지점에서의 기울기는 구할 수 있다.
아래와 같은 수식의 [-3, 3] 구간에서의 최소값을 찾아보며 경사하강법에 대해 이해해보자.
\[y = \frac{1}{3}x^3 - 4x\]1
2
3
4
5
6
7
8
9
def func(x):
y = (1/3)*(x**3) - 4*x
return y
h = 1e-3 # = 0.001
x_max = 3
x_min = -3
x = np.arange(x_min, x_max, h)
x의 초기값 지정
이 방법을 사용하는 데 있어서 가장 중요한 일은 초기값의 지정이다. 초기값에 따라 결과값이 다를 수 있기 때문이다. 지금은 x=0일때 y=0이므로, x=0 근처에 최소값이 있을 것이라고 가정하고 이를 초기값으로 지정한다.
1
x0 = 0
기울기 계산
이 초기값에 대해서 기울기를 계산해 보자.
1
2
3
4
5
6
def diff(x):
global h
tangent = (func(x+h)-func(x))/h
return tangent
print(diff(x0))
이렇게 f’(0)을 구할 수 있고, 그 결과값은 -3.9999…로 약 -4이다. 이 기울기가 0보다 작은 음수라는 것은 x가 증가함에 따라 y는 감소하는 중임을 의미한다.
x를 변경
1
2
3
4
5
step = 1e-3
def update(x):
global step
return x - np.sign(diff(x))*step
우리는 x=0에서 이 함수가 감소 중임을 알고 있다. 그렇다면 x를 약간 증가시켜서, 감소 중인 방향으로 나아가다 보면 최소값을 얻을 수 있을 것이다.
이에 착안해, 함수가 감소 중(=기울기가 음수)일때는 x를 약간 증가시키고, 함수가 증가 중(=기울기가 양수)일때는 x를 약간 감소시킨다. 즉 x가 커짐에 따라 y가 증가하는 경우에는 이와 반대로 움직여서 y가 감소하는 방향으로 움직인다.
주어진 코드는 기울기의 부호 * step을 빼주고 있는데, 기울기가 양수일 때는 약간 줄어든 값을 반환하고 기울기가 음수일 때는 약간 증가한 값을 반환한다.
step은 아주 작은 값이다. 이 step을 어떤 크기로 정하는지도 이 방법의 정확성에 중요한 요소이다.
반복 후 수렴
1
2
3
4
5
6
7
8
9
10
11
x_ = update(x0)
while np.abs(diff(x_)) >= convergence:
x_ = update(x_)
# 구간 제한
if x_ < x_min:
x_ = x_min
break
if x_ > x_max:
x_ = x_max
break
앞서 있었던 기울기를 계산하고 x를 변경하는 과정을 반복한다. 이 과정은 내가 원하는 수준의 정확도를 얻을 때까지 계속해서 반복한다. 현재 위치에서의 기울기가 어느정도 되는지를 평가하고, 이것이 0에 충분히 가까우면 (= 최소값에 가까워지면) 반복을 중단한다. 이때의 x값에 따른 f(x)가 최소값이라고 할 수 있겠다.
정리 및 결과
앞서 설명한 과정을 하나로 모아 주어진 수식의 최소값을 다음과 같이 구할 수 있다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
import numpy as np
import matplotlib.pyplot as plt
def func(x):
y = (1/3)*(x**3) - 4*x
return y
def diff(x):
global h
tangent = (func(x+h)-func(x))/h
return tangent
def update(x):
global step
return x - np.sign(diff(x))*step
h = 1e-3 # = 0.001
step = 1e-3
convergence = 1e-2
x_max = 3
x_min = -3
x = np.arange(x_min, x_max, h)
x0 = 0
x_ = update(x0)
while np.abs(diff(x_)) >= convergence:
x_ = update(x_)
# 구간 제한
if x_ < x_min:
x_ = x_min
break
if x_ > x_max:
x_ = x_max
break
plt.title('Gradient descent with x0 = ' + str(x0))
plt.plot(x, func(x)) # Basic graph
plt.scatter(x0, func(x0), color='blue')
plt.scatter(x_, func(x_), color='red')
plt.grid()
plt.show()
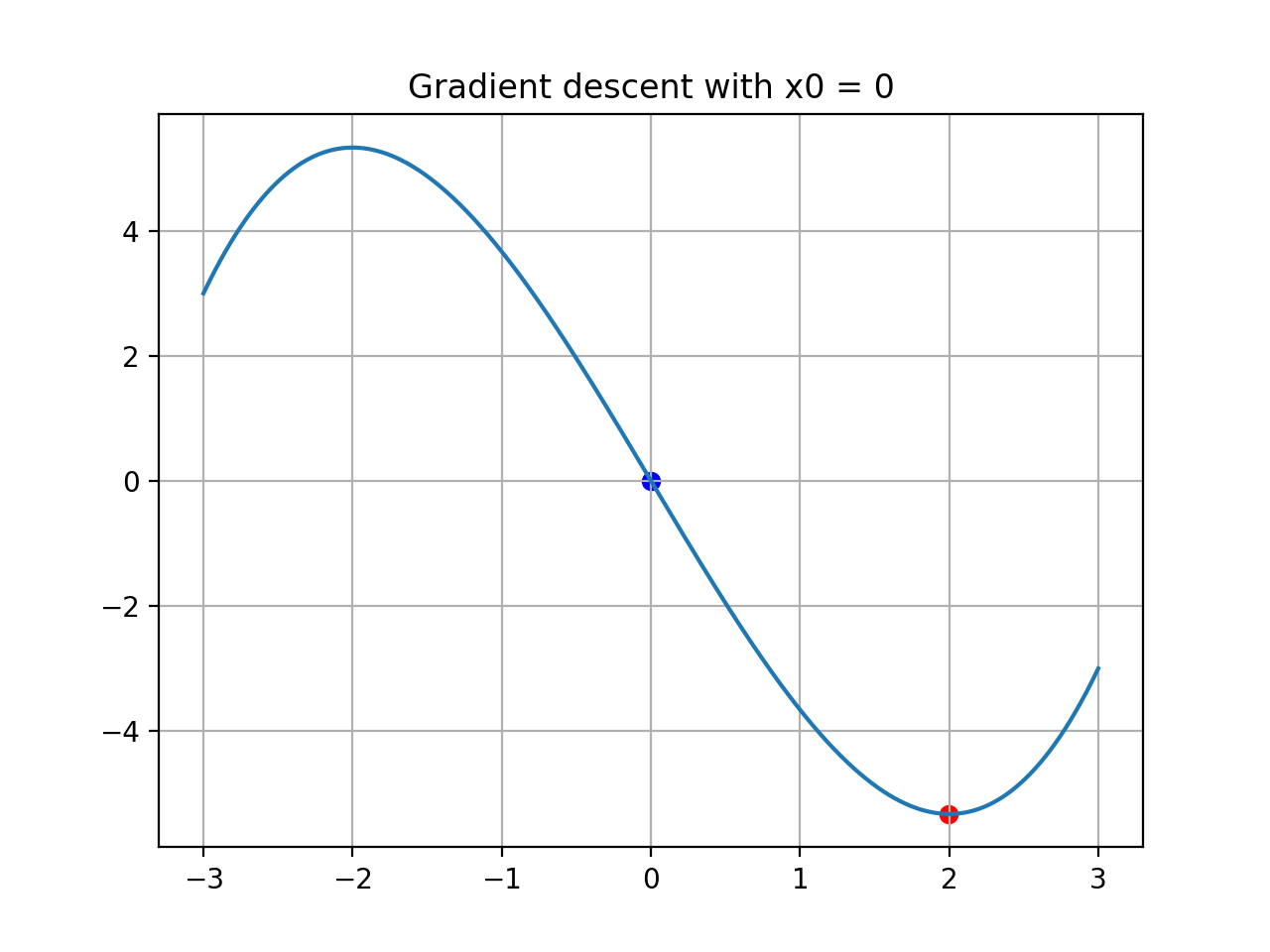
위 과정을 통해 구한 (x_, func(_x))에 찍은 점이 실제 최소값과 일치함을 확인할 수 있다.
초기값 지정의 중요성
앞서 초기값에 따라 결과값이 달라질 수 있다고 이야기했는데, 아래 수식에 대해 초기값을 다르게 지정해보며 자세히 알아보자.
\[y = \frac{sin(x)}{x}\]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
import numpy as np
import matplotlib.pyplot as plt
def func(x):
y = np.sin(x) / x
return y
def diff(x):
global h
tangent = (func(x+h)-func(x))/h
return tangent
def update(x):
global step
return x - np.sign(diff(x))*step
h = 1e-3 # = 0.001
step = 1e-3
convergence = 1e-2
x_max = 15
x_min = 1e-3 # 0으로 나눌 수 없음
x = np.arange(x_min, x_max, h)
x0 = 1
x_ = update(x0)
while np.abs(diff(x_)) >= convergence:
x_ = update(x_)
# 구간 제한
if x_ < x_min:
x_ = x_min
break
if x_ > x_max:
x_ = x_max
break
plt.title('Gradient descent with x0 = ' + str(x0))
plt.plot(x, func(x)) # Basic graph
plt.scatter(x0, func(x0), color='blue')
plt.scatter(x_, func(x_), color='red')
plt.grid()
plt.show()
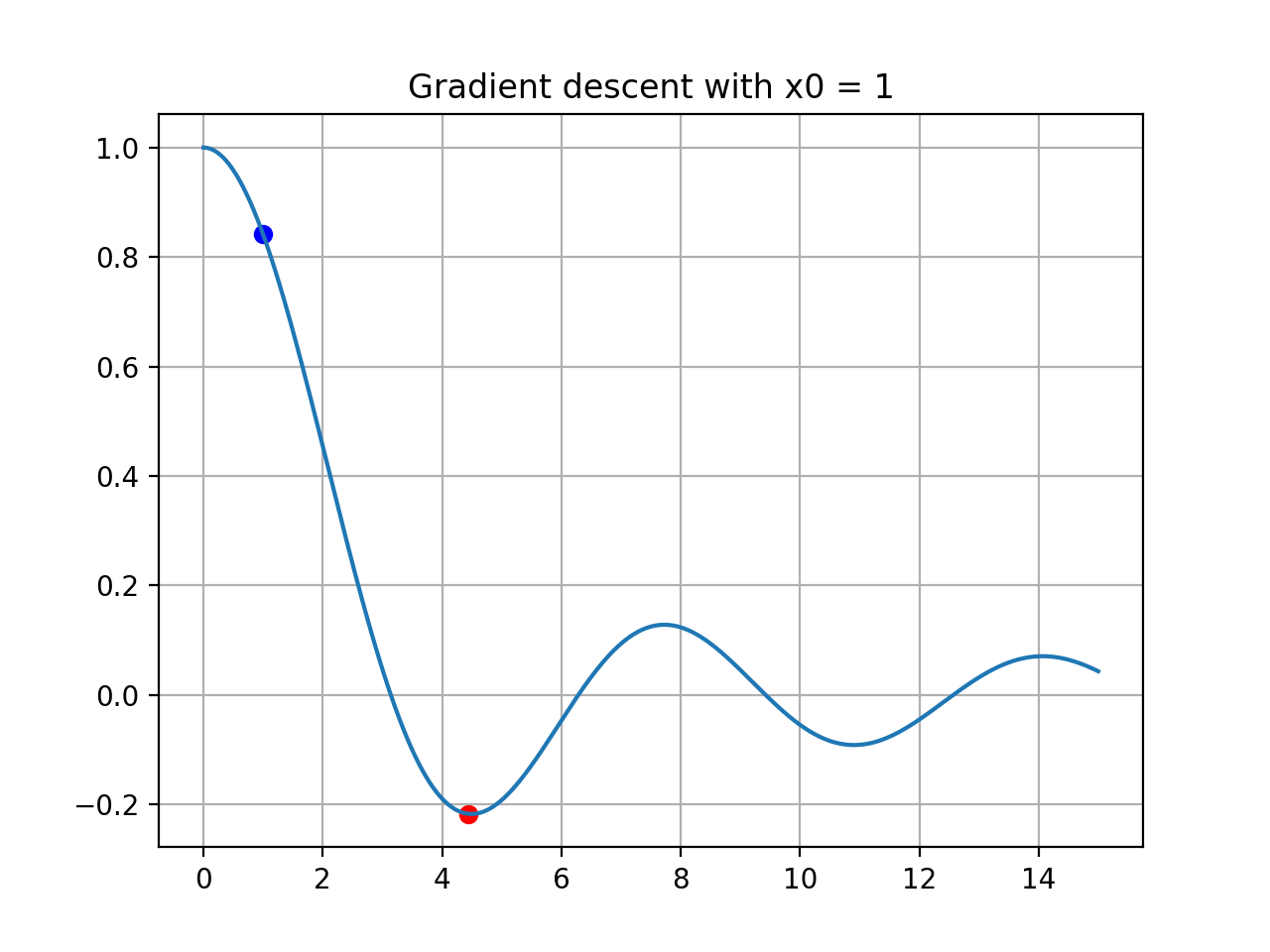
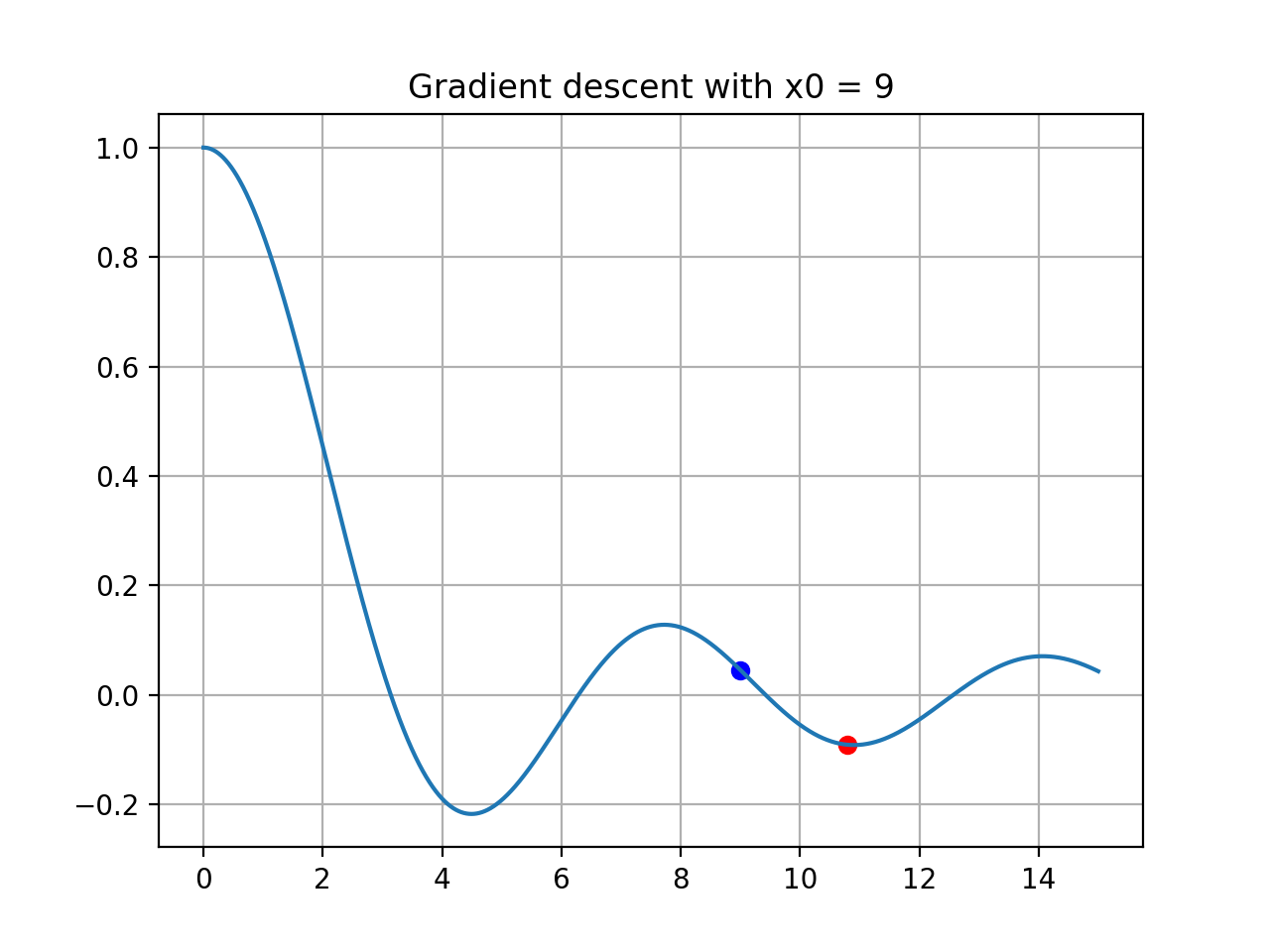
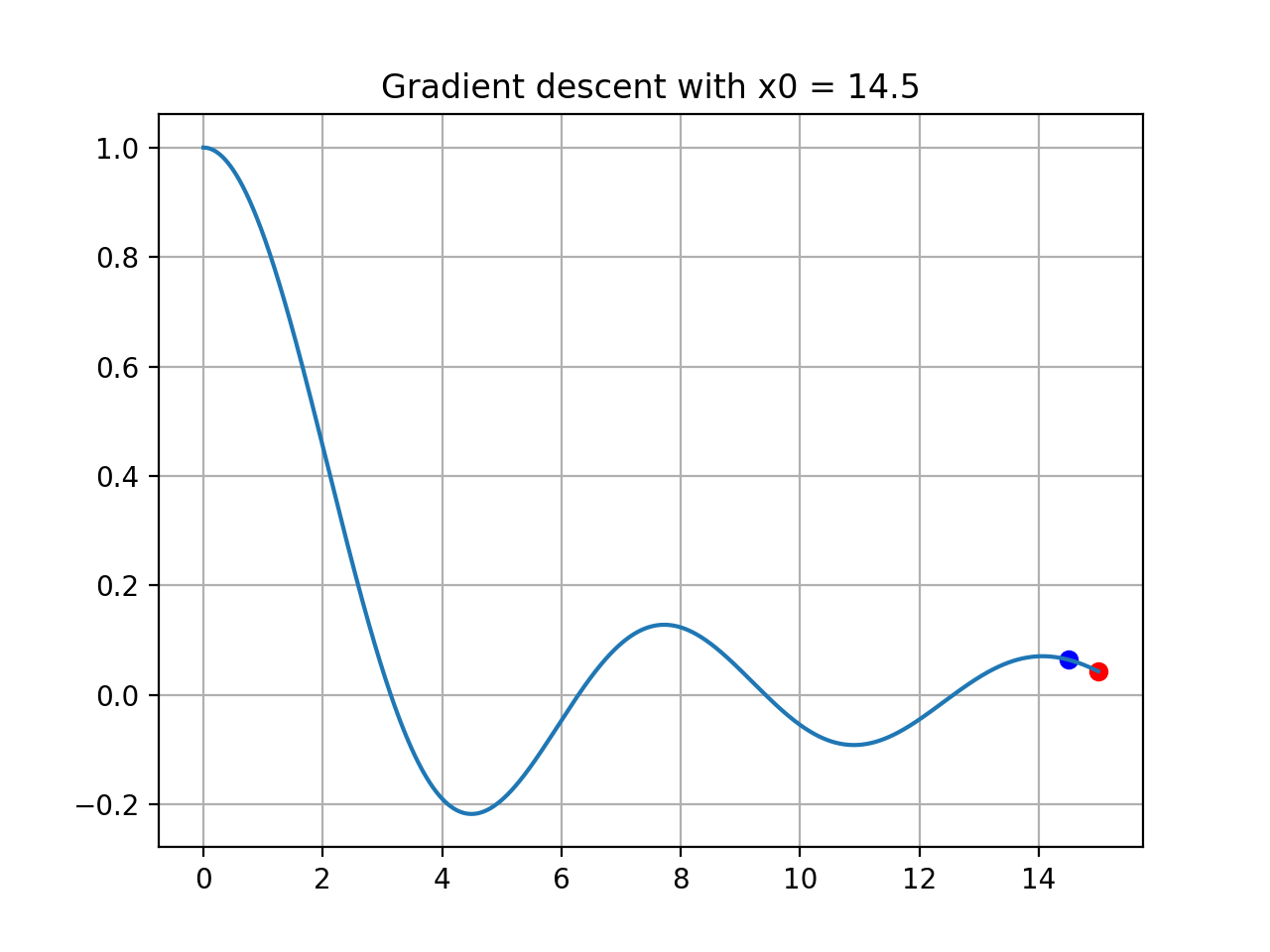
위와 같이 초기 위치에 따라서 다른 결과값이 나오는 모습을 확인할 수 있다.
왜 이런 현상이 발생했을까? 그것은 경사하강법 알고리즘이 미분값을 통해 현재 위치에서 함수값을 감소시키는 방향으로 움직이기 때문이다.
위 그림 중 초기 위치가 9에서 시작하는 경우, 실제 최소값이 위치한 방향으로 가기 위해서는 왼쪽으로 움직여야 하지만, 9의 위치에서 기울기에 따라 함수값이 감소하는 방향은 오른쪽이기 때문에 x가 계속 증가하여 그 부근의 극소값으로 수렴하게 된 것이다.
이런 이유로 인해서 경사하강법을 사용하는데에는 초기값의 지정이 매우 중요하다고 할 수 있겠다.
의미
경사하강법을 통해서 함수의 최소값을 찾아낼 수 있으며, 이는 신경망의 손실(Loss)의 최소값 역시 찾아낼 수 있음을 의미한다. 다음에는 이를 통해 신경망에서 어떻게 손실을 줄이는 학습 과정이 이루어지는지 알아보겠다.