개요
Multi Layer Perceptron 구조의 신경망에서 한 Layer가 다음 Layer로 결과값을 전달해 나가는 과정에 대해서 알아본다.
신호 전달하기
표기법
입력 Layer는 0층으로 보며, 아래 그림의 경우 2개의 Hidden Layer를 각각 1층, 2층으로 본다. 마지막 Output Layer를 3층으로 보아 아래 그림은 3층 신경망을 보여주고 있다. 즉, 신경망의 층 수는 입력 Layer를 제외한 Layer 개수로 보면 되겠다.
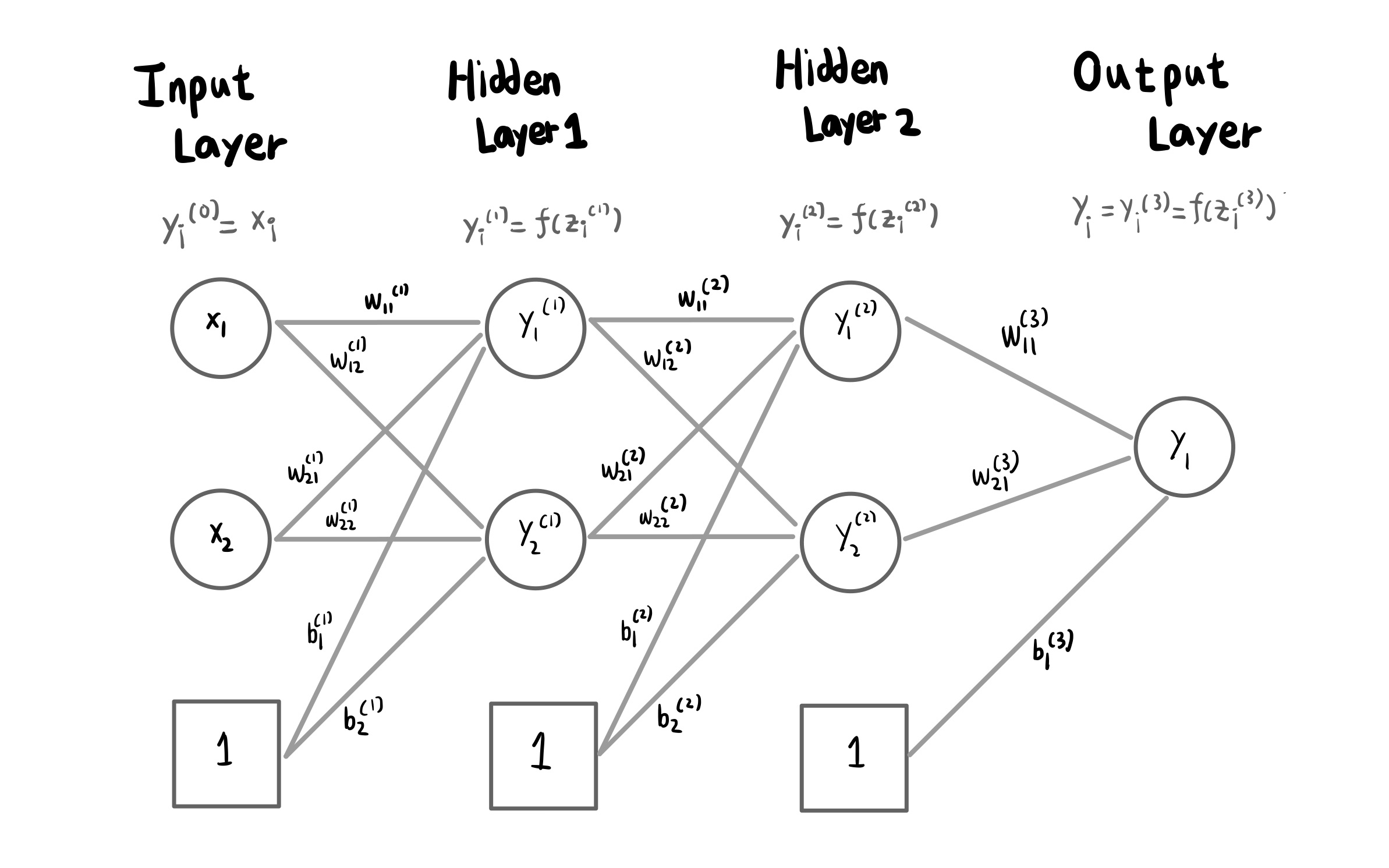
위 그림을 통해서 신경망에서 신호가 전달되는 구조와 그 수학적 표기를 그려 보았다.
\(w_{ij}^{(k)} \; y_i^{(k)} \; b_j^{(k)}\) 에서 k는 이 가중치가 적용되는 Layer의 층 수, i와 j는 각각 이번 층과 다음 층에서 몇번째 퍼셉트론인지를 의미한다. w는 가중치 (Weight), y는 결과값, b는 편향 (Bias) 를 나타낸다.
계산하는 법
위 그림에서 1층의 첫번쨰 뉴런의 계산 결과값 y_1^(1)과 y_2^(1) 을 계산해보고자 한다.
\[y_1^{(1)} = f(z_1^{(1)}), \; z_1^{(1)} = w_{11}^{(1)}x_1 + w_{21}^{(1)}x_2 + b_1^{(1)} = \sum_i w_{i1}^{(1)}x_i + b_1^{(1)} \\ y_2^{(1)} = f(z_2^{(1)}), \; z_2^{(1)} = w_{12}^{(1)}x_1 + w_{22}^{(1)}x_2 + b_2^{(1)} = \sum_i w_{i1}^{(1)}x_i + b_2^{(1)}\]우리는 이 식을 다음과 같이 행렬을 이용해서 정리할 수 있다.
\[\textbf{Z}^{(1)} = \textbf{X}^{(1)} \cdot \textbf{W}^{(1)} + \textbf{B}^{(1)}\] \[where \\ \textbf{Z}^{(1)} =\begin{bmatrix} z_1^{(1)} z_2^{(1)} \end{bmatrix} \; \textbf{X}^{(1)} = \begin{bmatrix}x_1 x_2 \end{bmatrix} \; \textbf{W}^{(1)} = \begin{bmatrix}w_{11}^{(1)} & w_{21}^{(1)} \\w_{12}^{(1)} & w_{22}^{(1)} \end{bmatrix} \; \textbf{B}^{(1)} = \begin{bmatrix} b_1^{(1)} b_2^{(1)} \end{bmatrix}\]이렇게 행렬을 이용하면, 파이썬의 numpy 패키지가 곱셈 및 덧셈 등 행렬에 대한 연산을 지원하기 때문에 코드가 간결해지며 동작 역시 빨라지는 효과가 있다.
Affine combination을 행렬을 통해서 계산한 뒤, 행렬의 각 요소에 지난 포스트에서 보았던 다양한 Activation 함수를 적용한다. 이렇게 하여 한 층의 계산 결과를 얻을 수 있다.
\[\textbf{Y}^{(1)} =\begin{bmatrix} f(z_1^{(1)}) \; f(z_2^{(1)}) \end{bmatrix}\]1층에서 2층으로 넘어가는 과정에서는 1층의 계산 결과물이 새로운 입력이 된다.
\[\textbf{Z}^{(2)} = \textbf{Y}^{(1)} \cdot \textbf{W}^{(2)} + \textbf{B}^{(2)} \\ \textbf{Y}^{(2)} =\begin{bmatrix} f(z_1^{(2)}) \; f(z_2^{(2)}) \end{bmatrix}\]마찬가지로, 2층에서 출력층인 3층으로 넘어가는 과정에서도 2층의 계산 결과물을 입력으로 삼는다. 그런데 입력->1층이나 1층->2층과는 달리 2개의 퍼셉트론이 하나의 퍼셉트론으로 연결되어 있으므로, 가중치의 개수가 기존과 다르다.
\[\textbf{Z}^{(3)} = \textbf{Y}^{(2)} \cdot \textbf{W}^{(3)} + \textbf{B}^{(3)}\] \[where \\ \textbf{Z}^{(3)} =\begin{bmatrix} z_1^{(3)} \end{bmatrix} \; \textbf{Y}^{(2)} = \begin{bmatrix}y_1^{(2)} y_2^{(2)} \end{bmatrix} \; \textbf{W}^{(3)} = \begin{bmatrix}w_{11}^{(1)} \\w_{12}^{(1)} \end{bmatrix} \; \textbf{B}^{(3)} = \begin{bmatrix} b_1^{(3)} \end{bmatrix}\]마찬가지로 최종 출력은 Activation 함수를 거쳐서 나온다.
\[\textbf{Y}^{(3)} = f(z_1^{(3)})\]결론
MLP에서 입력이 은닉층 (Hidden Layer)을 거쳐 출력으로 나오는 과정을 살펴 보았다. 앞으로는 이 출력을 정답과 비교하여 고쳐나가는 학습 과정에 대해서 알아보고자 한다.